
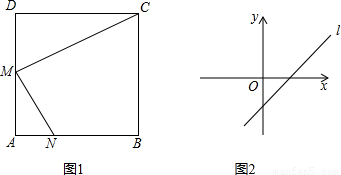
 ;
;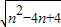 -|m-1|=m-n-(2-n)-(m-1)(7分)
-|m-1|=m-n-(2-n)-(m-1)(7分) a时,△CDM∽△MAN.(2分)
a时,△CDM∽△MAN.(2分) a,(4分)
a,(4分)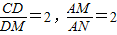 ,(6分)
,(6分)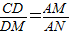 (7分)
(7分)

科目:初中数学 来源:2006年四川省乐山市中考数学试卷(课标卷)(解析版) 题型:填空题
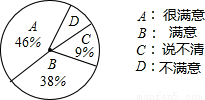 (2006•乐山)某商场为了了解本商场的服务质量,随机调查了要商场的100名顾客,调查的结果如图所示,根据图中给出的信息,这100名顾客中对商场的服务质量不满意的有 人.
(2006•乐山)某商场为了了解本商场的服务质量,随机调查了要商场的100名顾客,调查的结果如图所示,根据图中给出的信息,这100名顾客中对商场的服务质量不满意的有 人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com