
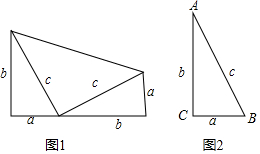
���� ̽�����֣��ò�ͬ�ķ�������ͼ1����������Է���a��b��c����ʲô������ϵ��
����Ӧ�ã�������֪������̽�����ֵĹ��ɣ���������ε��ܳ�������Ķ�����⣻
�ڸ�������õ�������$\left\{\begin{array}{l}{c+a=144}\\{c-a=1}\end{array}\right.$��$\left\{\begin{array}{l}{c+a=72}\\{c-a=2}\end{array}\right.$��$\left\{\begin{array}{l}{c+a=48}\\{c-a=3}\end{array}\right.$��$\left\{\begin{array}{l}{c+a=36}\\{c-a=4}\end{array}\right.$��$\left\{\begin{array}{l}{c+a=24}\\{c-a=6}\end{array}\right.$��$\left\{\begin{array}{l}{c+a=18}\\{c-a=8}\end{array}\right.$��$\left\{\begin{array}{l}{c+a=16}\\{c-a=9}\end{array}\right.$���ⷽ���鼴����⣮
��� �⣺̽�����֣�
ͼ1�����=$\frac{1}{2}$ab��2+$\frac{1}{2}$c2=ab+$\frac{1}{2}$c2��
ͼ1�����=$\frac{1}{2}$��a+b����a+b��=$\frac{1}{2}$��a+b��2��
ab+$\frac{1}{2}$c2=$\frac{1}{2}$��a+b��2��
ab+$\frac{1}{2}$c2=$\frac{1}{2}$��a2+2ab+b2����
$\frac{1}{2}$c2=$\frac{1}{2}$a2+$\frac{1}{2}$b2��
a2+b2=c2��
����Ӧ�ã�
����������$\left\{\begin{array}{l}{b-a=2}\\{{a}^{2}+{b}^{2}=1{0}^{2}}\end{array}\right.$��
���$\left\{\begin{array}{l}{ab=48}\\{a+b=14}\end{array}\right.$��$\left\{\begin{array}{l}{ab=48}\\{a+b=-14}\end{array}\right.$����ȥ����
�ʴ������ε��ܳ���14+10=24�������48��2=24��
����������
$\left\{\begin{array}{l}{c+a=144}\\{c-a=1}\end{array}\right.$�����$\left\{\begin{array}{l}{c=72.5}\\{a=71.5}\end{array}\right.$����ȥ����
$\left\{\begin{array}{l}{c+a=72}\\{c-a=2}\end{array}\right.$�����$\left\{\begin{array}{l}{c=37}\\{a=35}\end{array}\right.$��
$\left\{\begin{array}{l}{c+a=48}\\{c-a=3}\end{array}\right.$�����$\left\{\begin{array}{l}{c=25.5}\\{a=22.5}\end{array}\right.$����ȥ����
$\left\{\begin{array}{l}{c+a=36}\\{c-a=4}\end{array}\right.$�����$\left\{\begin{array}{l}{c=20}\\{a=16}\end{array}\right.$��
$\left\{\begin{array}{l}{c+a=24}\\{c-a=6}\end{array}\right.$�����$\left\{\begin{array}{l}{c=15}\\{a=9}\end{array}\right.$��
$\left\{\begin{array}{l}{c+a=18}\\{c-a=8}\end{array}\right.$�����$\left\{\begin{array}{l}{c=13}\\{a=5}\end{array}\right.$
$\left\{\begin{array}{l}{c+a=16}\\{c-a=9}\end{array}\right.$�����$\left\{\begin{array}{l}{c=12.5}\\{a=3.5}\end{array}\right.$����ȥ����
����������������a��c��ֵΪa=35��c=37��a=16��c=20�� a=5��c=13��a=9��c=15��
���� �����˹��ɶ�����֤���������ε��ܳ�������������ѵ��ǵڣ�3���ʣ��ؼ��ǵõ�����a��c�ķ����飮


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2.5��106 | B�� | 2.5��10-6 | C�� | 2.5��107 | D�� | 2.5��10-7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
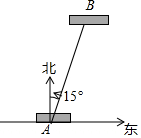 ��ͼ��һ�Ҵ���A�����պ������50 ����λ��B���ľ������������÷���;����������մ�����ھ�������λ����ƫ��15�㣬50���
��ͼ��һ�Ҵ���A�����պ������50 ����λ��B���ľ������������÷���;����������մ�����ھ�������λ����ƫ��15�㣬50����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
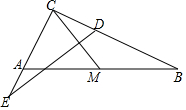 ��ͼ����M��Rt��ABC��б��AB���е㣬����CM�����߶�CM�Ĵ�ֱƽ���ߣ��ֱ�CB��CA���ӳ����ڵ�D��E������C=90�㣬AB=20��tanB=$\frac{2}{5}$����DE=$\frac{29}{2}$��
��ͼ����M��Rt��ABC��б��AB���е㣬����CM�����߶�CM�Ĵ�ֱƽ���ߣ��ֱ�CB��CA���ӳ����ڵ�D��E������C=90�㣬AB=20��tanB=$\frac{2}{5}$����DE=$\frac{29}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
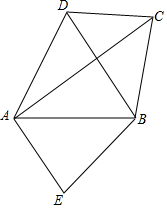 ��ABC�У���ACB��90�㣬��ABΪһ�����ȱߡ�ABD���ҵ�D���C��ֱ��ABͬ�࣬ƽ������һ��E���D�ֱ���ֱ��AB���࣬��BE=BC����ABE=��DBC������CD��AE��AC=5��BC=3��
��ABC�У���ACB��90�㣬��ABΪһ�����ȱߡ�ABD���ҵ�D���C��ֱ��ABͬ�࣬ƽ������һ��E���D�ֱ���ֱ��AB���࣬��BE=BC����ABE=��DBC������CD��AE��AC=5��BC=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
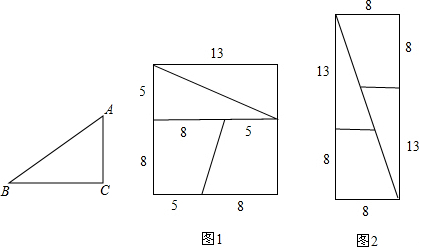
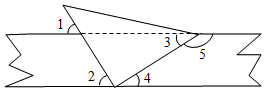 ��һֱ�����ǰ�������ƽ�е�ֽ������ͼ��ʾ���ã����н��ۣ�
��һֱ�����ǰ�������ƽ�е�ֽ������ͼ��ʾ���ã����н��ۣ�| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com