
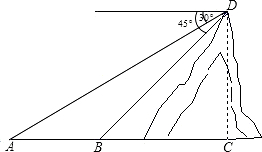
 边防战士在海拔高度为50米(即CD的长)的小岛顶部D处执行任务,上午8点,发现在海面上的A处有一艘船,此时测得该船的俯角为30°,该船沿着AC方向航行一段时间后到达B处,又测得该船的俯角为45°,求该船在这一段时间内的航程.
边防战士在海拔高度为50米(即CD的长)的小岛顶部D处执行任务,上午8点,发现在海面上的A处有一艘船,此时测得该船的俯角为30°,该船沿着AC方向航行一段时间后到达B处,又测得该船的俯角为45°,求该船在这一段时间内的航程.科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
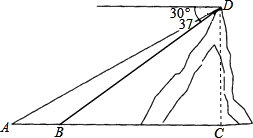 如图,我边防战士在海拔高度(即CD的长)为60米的小岛顶部D执行任务,上午8时发现在海面上的A处有一艘船,此时测得该船的俯角为30°,该船沿着AC方向航行一段时间后到达B处,此时测得该船的俯角为37°,求该船在这段时间内的航程.(sin37°=
如图,我边防战士在海拔高度(即CD的长)为60米的小岛顶部D执行任务,上午8时发现在海面上的A处有一艘船,此时测得该船的俯角为30°,该船沿着AC方向航行一段时间后到达B处,此时测得该船的俯角为37°,求该船在这段时间内的航程.(sin37°=| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
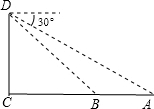 (2007•西城区二模)边防战士在海拔高度为50米(即CD的长)的小岛顶部D处执行任务,上午8点,发现在海面上的A处有一艘船,此时测得该船的俯角为30°,该船沿着AC方向航行一段时间后到达B处,又测得该船的俯角为45°,求该船在这一段时间内的航程.
(2007•西城区二模)边防战士在海拔高度为50米(即CD的长)的小岛顶部D处执行任务,上午8点,发现在海面上的A处有一艘船,此时测得该船的俯角为30°,该船沿着AC方向航行一段时间后到达B处,又测得该船的俯角为45°,求该船在这一段时间内的航程.查看答案和解析>>
科目:初中数学 来源:2007年北京市西城区中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com