解答:解:①设从4点整时针顺时针转过a角后,时针与分针(分针在时钟前)成120°,则
12a=120+a+120,
a=21
.
由于时针每转过30°(如从指向数字4转到指向数字5)相当于1小时(60分钟),
21
×2=43
分钟.
故在4点43
分时,时针与分针成120°;
②设从4点43
分时针顺时针转过a角后,时针与分针(分针在时钟后)成120°,则
12a=a+(240-120),
a=10
.
由于时针每转过30°(如从指向数字4转到指向数字5)相当于1小时(60分钟),
10
×2=21
分钟.
故在4点43
+21
分=5点5
分时,时针与分针成120°;
③设从5点5
分时针顺时针转过a角后,时针与分针(分针在时钟前)成120°,则
12a=120+a+120,
a=21
.
由于时针每转过30°(如从指向数字4转到指向数字5)相当于1小时(60分钟),
21
×2=43
分钟.
故在5点5
分+43
分=5点49
分时,时针与分针成120°.
即在4点43
分,5点5
分,5点49
分时,时针与分针何时成120°角.
点评:本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动(
)°,并且利用起点时间时针和分针的位置关系建立角的图形.转化为方程解决.由于时针与分针所成角依时针与分针的“前”“后”次序有两种情况,因此,求两针夹角情况会出现多解.



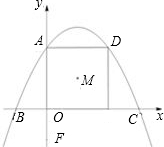 Q以某一速度沿FA方向运动,当点P运动时间t=1.5时,∠PDQ=45°,求点Q的运动速度.
Q以某一速度沿FA方向运动,当点P运动时间t=1.5时,∠PDQ=45°,求点Q的运动速度. x2+
x2+ x+4交y轴于A,分别交X轴的负半轴、正半轴于B、C两点,过点A作AD∥x轴交抛物线于点D,过点D作DE⊥x轴,垂足为点E.点M是四边形OADE的对角线的交点,点F在y轴负半轴上,且F(0,-2).
x+4交y轴于A,分别交X轴的负半轴、正半轴于B、C两点,过点A作AD∥x轴交抛物线于点D,过点D作DE⊥x轴,垂足为点E.点M是四边形OADE的对角线的交点,点F在y轴负半轴上,且F(0,-2).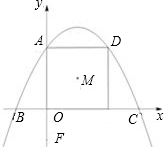 Q以某一速度沿FA方向运动,当点P运动时间t=1.5时,∠PDQ=45°,求点Q的运动速度.
Q以某一速度沿FA方向运动,当点P运动时间t=1.5时,∠PDQ=45°,求点Q的运动速度.