
 如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
 ;
; ;
;
 a-x
a-x
 ,
, ;
; a2,
a2, a2.
a2. ,由图知,16开纸的长边是1开纸的长边和四分之一,16开纸的短边也是1开纸的短边和四分之一,故AD=
,由图知,16开纸的长边是1开纸的长边和四分之一,16开纸的短边也是1开纸的短边和四分之一,故AD= a,AB=
a,AB= a;
a; a,由折叠的性质知,“2开”纸的短边是1开纸的长边的一半,长边是1开纸的短边,“4开”纸的短边是2开纸的长边的一半,长边是2开纸的短边,“8开”纸的短边是4开纸的长边的一半,长边是4开纸的短边,故“2开”纸,“4开”纸,“8开”纸的长与宽之比都相等都等于
a,由折叠的性质知,“2开”纸的短边是1开纸的长边的一半,长边是1开纸的短边,“4开”纸的短边是2开纸的长边的一半,长边是2开纸的短边,“8开”纸的短边是4开纸的长边的一半,长边是4开纸的短边,故“2开”纸,“4开”纸,“8开”纸的长与宽之比都相等都等于 ;
; ,得CF=2DG=2x.
,得CF=2DG=2x. ,求解即为DG的值.
,求解即为DG的值.
 a,
a, a,如图,梯形有两种情况,①如左图,MN=MQ=2QP=
a,如图,梯形有两种情况,①如左图,MN=MQ=2QP= a,则它的面积=
a,则它的面积= (MN+PQ)•MQ=
(MN+PQ)•MQ= a2.
a2. a=
a= a,AQ=
a,AQ=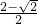 a,AM=(
a,AM=( -1)a.由勾股定理知,MQ2=AM2+AQ2=
-1)a.由勾股定理知,MQ2=AM2+AQ2= a,
a, (MN+PQ)•MQ=
(MN+PQ)•MQ= a2.
a2.

科目:初中数学 来源: 题型:
 如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
查看答案和解析>>
科目:初中数学 来源:第4章《相似三角形》常考题集(11):4.3 两个三角形相似的判定(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第24章《相似形》中考题集(20):24.3 相似三角形的性质(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《图形的对称》(05)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《三角形》(16)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com