Question

已知：如图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关______；
（2）仔细观察，在图2中“8字形”的个数：______个；
（3）在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．利用（1）的结论，试求∠P的度数；
（4）如果图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结论即可）

Answer 1

解：（1）在△AOD中，∠AOD=180°-∠A-∠D，
在△BOC中，∠BOC=180°-∠B-∠C，
∵∠AOD=∠BOC（对顶角相等），
∴180°-∠A-∠D=180°-∠B-∠C，
∴∠A+∠D=∠B+∠C；

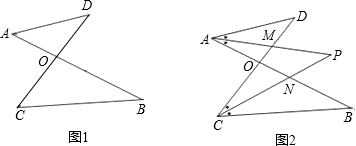
（2）交点有点M、O、N，
以M为交点有1个，为△AMD与△CMP，
以O为交点有4个，为△AOD与△COB，△AOM与△CON，△AOM与△COB，△CON与△AOD，
以N为交点有1个，为△ANP与△CNB，
所以，“8字形”图形共有6个；

（3）∵∠D=40°，∠B=36°，
∴∠OAD+40°=∠OCB+36°，
∴∠OCB-∠OAD=4°，
∵AP、CP分别是∠DAB和∠BCD的角平分线，
∴∠DAM=∠OAD，∠PCM=∠OCB，
又∵∠DAM+∠D=∠PCM+∠P，
∴∠P=∠DAM+∠D-∠PCM=（∠OAD-∠OCB）+∠D=×（-4°）+40°=38°；


（4）根据“8字形”数量关系，∠OAD+∠D=∠OCB+∠B，∠DAM+∠D=∠PCM+∠P，
所以，∠OCB-∠OAD=∠D-∠B，∠PCM-∠DAM=∠D-∠P，
∵AP、CP分别是∠DAB和∠BCD的角平分线，
∴∠DAM=∠OAD，∠PCM=∠OCB，
∴（∠D-∠B）=∠D-∠P，
整理得，2∠P=∠B+∠D．
分析：（1）利用三角形的内角和定理表示出∠AOD与∠BOC，再根据对顶角相等可得∠AOD=∠BOC，然后整理即可得解；
（2）根据“8字形”的结构特点，根据交点写出“8字形”的三角形，然后确定即可；
（3）根据（1）的关系式求出∠OCB-∠OAD，再根据角平分线的定义求出∠DAM-∠PCM，然后利用“8字形”的关系式列式整理即可得解；
（4）根据“8字形”用∠B、∠D表示出∠OCB-∠OAD，再用∠D、∠P表示出∠DAM-∠PCM，然后根据角平分线的定义可得∠DAM-∠PCM=（∠OCB-∠OAD），然后整理即可得证．
点评：本题考查了三角形内角和定理，角平分线的定义，多边形的内角和定理，对顶角相等的性质，整体思想的利用是解题的关键．