解:(1)连接O
1A,O
2B,
∵O
1M=O
1A,
∴∠O
1AM=∠O
1MA,
同理∠O
2BN=∠O
2NB,
∵∠C=90°,
∴∠CMN+∠CNM=90°,∠CAB+∠CBA=90°,
∵∠O
1MA=∠CMN,∠O
2NB=∠CNM,
∴∠O
1MA+∠O
2NB=90°,
∴∠O
1AM+∠O
2BN=90°,
∴∠O
1AB+∠O
2BA=∠O
1AM+∠CAB+∠CBA+∠O
2BN=180°,
∴O
1A∥O
2B;
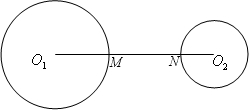
(2)由(1)知O
1A∥O
2B,若又有AB∥O
1O
2,
则四边形O
1ABO
2为平行四边形,
∴O
1A=O
2B,即R=r,
∴R=r时,AB∥O
1O
2;
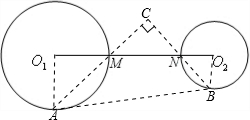
(3)存在点C.
点C的位置可以这样确定:
先作两圆的外公切线AB,然后连接AM、BN交于点C,
理由如下:
∵AB切圆O
1于点A,切圆O
2于点B,
∴O
1A⊥AB,O
2B⊥AB,
∴∠O
1AM+∠CAB=∠O
1AB=90°O
1A∥O
2B,
∴∠O
1+∠O
2=180°,
又∠O
1MA+∠O
1AM+∠O
1=180°,∠O
2NB+∠O
2BN+∠O
2=180°,
∠O
1AM=∠O
1MA,∠O
2BN=∠O
2NB,
∴∠O
1MA+∠O
2NB=90°,
∵∠O
1MA=∠CMN,∠O
2NB=∠CNM,
∴∠CMN+∠CNM=90°,
∴∠C=90°,
∵∠CMN=∠O
1MA=∠O
1AM,
而∠CMN+∠CNM=90°,∠O
1AM+∠CAB=90°,
∴∠CNM=∠CAB,
∴△CNM∽△CAB,
∴
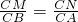
,
即CM•CA=CN•CB.
分析:(1)本题需先连接O
1A,O
2B,然后得出∠O
1AM=∠O
1MA和∠O
2BN=∠O
2NB,再根据∠O
1MA+∠O
2NB=90°,∠O
1AM+∠O
2BN=90°,证出∠O
1AB+∠O
2BA=180°,即可求出结果.
(2)本题需先证出四边形O
1ABO
2为平行四边形,得出R=r,即可求出结果.
(3)本题需先作两圆的外公切线AB,然后连接AM、BN交于点C,然后进行证明,即可求出答案.
点评:本题主要考查了切线的性质,在解题时要能根据题意作出辅助线,并灵活应用切线的性质以及相似三角形和平行四边形的有关知识进行证明是本题的关键.


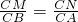 ,
,

 名校课堂系列答案
名校课堂系列答案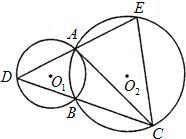 21、如图,已知⊙O1和⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,直线CB交⊙O1于点D,直线DA交⊙O2于点E.试证明:AC=EC.
21、如图,已知⊙O1和⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,直线CB交⊙O1于点D,直线DA交⊙O2于点E.试证明:AC=EC.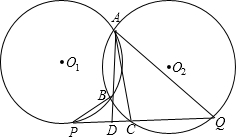 求S△ADC:S△ACQ的值.
求S△ADC:S△ACQ的值.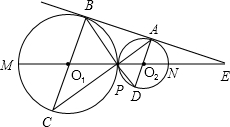 长线交⊙O1于C点,BP的延长线交⊙O2于D点,直线O1O2交⊙O1于M,交⊙O2于N,与BA的延长线交于点E.
长线交⊙O1于C点,BP的延长线交⊙O2于D点,直线O1O2交⊙O1于M,交⊙O2于N,与BA的延长线交于点E. 时它与⊙O1的位置关系是
时它与⊙O1的位置关系是