
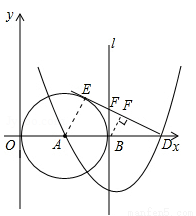
(12分)如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.

(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求DE的长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长 .
(1) ;(2)
;(2) ;(3)
;(3)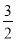 或
或 .
.
【解析】
试题分析:(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点坐标式,然后将C点坐标代入求解即可.
(2)由于DE是⊙A的切线,连接AE,那么根据切线的性质知AE⊥DE,在Rt△AED中,AE、AB是圆的半径,即AE=OA=AB=3,而A、D关于抛物线的对称轴对称,即AB=BD=3,由此可得到AD的长,进而可利用勾股定理求得切线DE的长.
(3)若△BFD与EAD△相似,则有两种情况需要考虑:①△AED∽△BFD,②△AED∽△FBD,根据不同的相似三角形所得不同的比例线段即可求得BF的长.
试题解析:(1)设抛物线的解析式为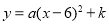 ;∵抛物线经过点A(3,0)和C(0,9),∴
;∵抛物线经过点A(3,0)和C(0,9),∴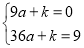 ,解得:
,解得: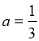 ,
,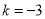 ,∴
,∴ ;
;
(2)连接AE;∵DE是⊙A的切线,∴∠AED=90°,AE=3,∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,∴AB=BD=3,∴AD=6;在Rt△ADE中, =
=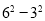 =27,∴DE=
=27,∴DE= ;
;
(3)当BF⊥ED时;∵∠AED=∠BFD=90°,∠ADE=∠BDF,∴△AED∽△BFD,∴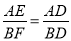 ,即
,即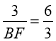 ,∴BF=
,∴BF=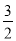 ;当FB⊥AD时,∵∠AED=∠FBD=90°,∠ADE=∠FDB,∴△AED∽△FBD,∴
;当FB⊥AD时,∵∠AED=∠FBD=90°,∠ADE=∠FDB,∴△AED∽△FBD,∴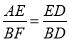 ,即BF=
,即BF=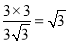 ;∴BF的长为
;∴BF的长为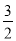 或
或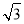 .
.
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年河北省九年级上学期第二次月考数学试卷(解析版) 题型:填空题
在比例尺为1:50000的地图上,量得甲、乙两地的距离是3cm,则甲、乙两地的实际距离是 m.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:选择题
若关于x的方程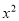 -m=2x有两个不相等的实数根,则m的取值范围是( )
-m=2x有两个不相等的实数根,则m的取值范围是( )
A.m>-1 B.m<-2 C.m≥0 D.m<0
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省九年级上学期期末考试数学试卷(解析版) 题型:解答题
(10分)如图,反比例函数 (
( )的图像过等边三角形AOB的顶点A,已知点B(-2,0).
)的图像过等边三角形AOB的顶点A,已知点B(-2,0).

(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图像上,需将△AOB向上平移多少个单位长度?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省九年级上学期期末考试数学试卷(解析版) 题型:选择题
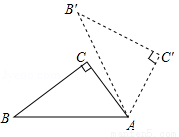
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校七年级上学期期中数学试卷(解析版) 题型:选择题
在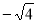 ,3.14 ,π,
,3.14 ,π,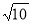 ,
,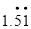 ,
,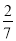 中无理数的个数是 ( )
中无理数的个数是 ( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com