
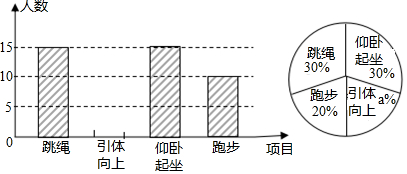
分析 (1)用整体1减去跳绳、仰卧起坐和跑步所占的百分比,即可求出a的值,再根据引体向上和跑步所占的百分比一样,即可得出引体向上的人数,从而补全统计图;
(2)用跳绳的人数除以所占的百分比即可得出该班学生人数;
(3)因为该班学生有50人,引体向上的有10人,根据概率公式直接得出答案.
解答 解:(1)a%=1-30%-30%-20%=20%,
则a=20;
∵引体向上和跑步所占的百分比一样,
∴引体向上的人数是10人,补图如下: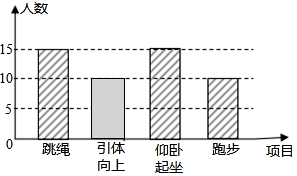 ;
;
故答案为:20;
(2)该班学生人数有$\frac{15}{30%}$=50(人);
(3)∵该班学生有50人,引体向上的有10人,
∴抽到参加了引体向上项目的学生的概率是$\frac{10}{50}$=$\frac{1}{5}$.
点评 此题考查了条形统计图、扇形统计图和概率公式,根据频数、频率和总数之间的关系求出该班学生总数是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
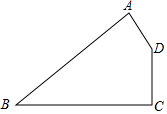 如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500$\sqrt{2}$米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500$\sqrt{2}$米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
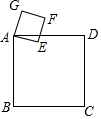 如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm.
如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
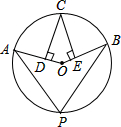 如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=36°,则∠P的度数为( )
如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=36°,则∠P的度数为( )| A. | 144° | B. | 72° | C. | 60° | D. | 36° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
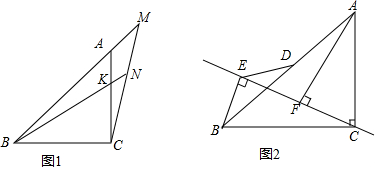
 如图中四边形ABCD是由两块完全重合的三角板拼成的,且AB=2,∠ACD=90°,∠DAC=30°,开始将一把直尺边EF放在与AC重叠的位置,再由此将直尺绕着AC中点P顺时针旋转角β,当直尺边EF与直线BD重叠时旋转就停止,在旋转过程中EF分别与线段BC、AD交于E、F.
如图中四边形ABCD是由两块完全重合的三角板拼成的,且AB=2,∠ACD=90°,∠DAC=30°,开始将一把直尺边EF放在与AC重叠的位置,再由此将直尺绕着AC中点P顺时针旋转角β,当直尺边EF与直线BD重叠时旋转就停止,在旋转过程中EF分别与线段BC、AD交于E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=$\frac{1}{2}$.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
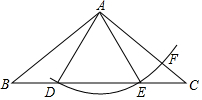 如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF.
如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com