
科目:初中数学 来源: 题型:
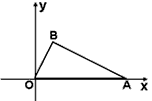
 如图Rt△ABC的斜边AC在直线l上,∠BAC=30°,BC=1.若将Rt△ABC以点C为中心顺时针旋转到如图所示位置,则点A运动到点A′所经过的路线长为
如图Rt△ABC的斜边AC在直线l上,∠BAC=30°,BC=1.若将Rt△ABC以点C为中心顺时针旋转到如图所示位置,则点A运动到点A′所经过的路线长为| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省昆明三中、滇池中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,Rt△ABO的顶点A是双曲线y= 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且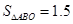 .(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出:(3)方程
.(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出:(3)方程 的解;(4)使一次函数的值大于反比例函数的值的
的解;(4)使一次函数的值大于反比例函数的值的 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源:2013届北京市三十一中学初三上学期期中考试数学试卷(带解析) 题型:解答题
如图,Rt△ABC的斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两直角边相切于点D、E,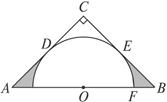
(1)求证∠A=∠B.
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市初三上学期期中考试数学试卷(解析版) 题型:解答题
如图,Rt△ABC的斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两直角边相切于点D、E,
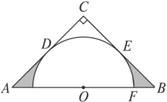
(1)求证∠A=∠B.
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com