
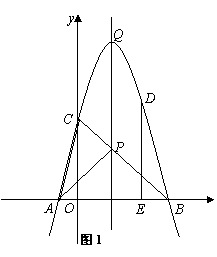
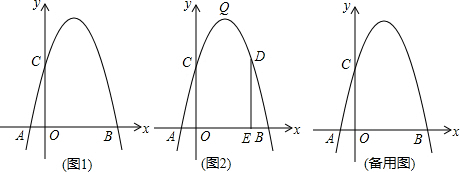
已知:如图1,抛物线![]() 的顶点为Q,与
的顶点为Q,与![]() 轴交于A(-1,0)、B(5,0)
轴交于A(-1,0)、B(5,0)
两点,与![]() 轴交于C点.
轴交于C点.
(1)求抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线的对称轴上求一点![]() ,使得△
,使得△![]() 的周长最小.请在图中画出点
的周长最小.请在图中画出点![]() 的位置,并求点
的位置,并求点![]() 的坐标;
的坐标;
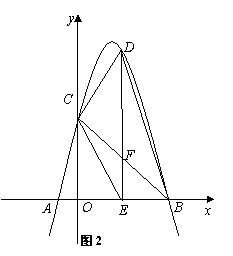
(3)如图2,若点D是第一象限抛物线上的一个动点,过D作DE⊥![]() 轴,垂足为E.
轴,垂足为E.
①有一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q与![]() 轴相距最远,所以当点D运动至点Q时,折线D-E-O的长度最长”。这个同学的说法正确吗?请说明理由.
轴相距最远,所以当点D运动至点Q时,折线D-E-O的长度最长”。这个同学的说法正确吗?请说明理由.
②若![]() 与直线
与直线![]() 交于点
交于点![]() .试探究:四边形
.试探究:四边形![]()
![]()
![]()
![]() 能否为平行四边形?
能否为平行四边形?
若能,请直接写出点![]() 的坐标;若不能,请简要说明理由;
的坐标;若不能,请简要说明理由;
 | |||||
 |  | ||||
解:(1)将A(-1,0)、B(5,0)分别代入![]() 中,
中,
得![]() ,得
,得![]() ∴
∴![]() .………………2分
.………………2分
 ∵
∵![]() , ∴Q(2 ,9).……3分
, ∴Q(2 ,9).……3分
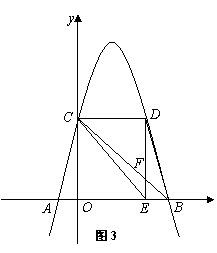
(2)如图1,连接BC,交对称轴于点P,连接AP、AC.……4分
∵AC长为定值,∴要使△PAC的周长最小,只需PA+PC最小.
∵点A关于对称轴![]() =1的对称点是点B(5,0),抛物线
=1的对称点是点B(5,0),抛物线![]() 与y轴交点C的坐标为(0,5).
与y轴交点C的坐标为(0,5).
![]() ∴由几何知识可知,PA+PC=PB+PC为最小. ………………5分
∴由几何知识可知,PA+PC=PB+PC为最小. ………………5分
设直线BC的解析式为y=k![]() +5,将B(5,0)代入5k+5=0,得k=-1,
+5,将B(5,0)代入5k+5=0,得k=-1,
∴![]() =-
=-![]() +5,∴当
+5,∴当![]() =2时,y=3 ,∴点P的坐标为(2,3). ….6分
=2时,y=3 ,∴点P的坐标为(2,3). ….6分
 (3) 这个同学的说法不正确. ……………7分
(3) 这个同学的说法不正确. ……………7分
∵设![]() ,设折线D-E-O的长度为L,则
,设折线D-E-O的长度为L,则
![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() .
.
而当点D与Q重合时,![]() ,
,
∴该该同学的说法不正确.…9分
(4)①四边形![]()
![]()
![]()
![]() 不能为平行四边形.……………10分
不能为平行四边形.……………10分
如图2,若四边形![]()
![]()
![]()
![]() 为平行四边形,则EF=DF,CF=BF.
为平行四边形,则EF=DF,CF=BF.
∵DE∥![]() 轴,∴
轴,∴![]() ,即OE=BE=2.5.
,即OE=BE=2.5.
 当
当![]() =2.5时,
=2.5时,![]() ,即
,即![]() ;
;
当![]() =2.5时,
=2.5时, ![]() ,即
,即![]() .
.
∴![]() >2.5. 即
>2.5. 即![]() >
>![]() ,这与EF=DF相矛盾,
,这与EF=DF相矛盾,
∴四边形![]()
![]()
![]()
![]() 不能为平行四边形. ……………12分
不能为平行四边形. ……………12分


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
| 5 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| ED+OP | ED•OP |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |

| 1 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com