
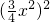 .
.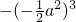 .
. .
.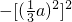 .
.科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
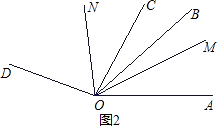
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 加数的个数n | 规律如下 |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
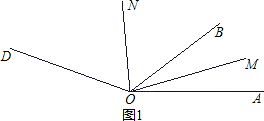
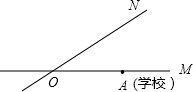 如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?
如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,路两旁50米内会受到噪音影响,已知有两台相距30米的拖拉机正沿ON方向行驶,它们的速度均为5米/秒,问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 PD,求△POD与△PDG的面积之比;
PD,求△POD与△PDG的面积之比;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com