
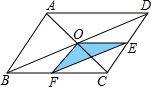
 如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么S△OEF:S平行四边形ABCD=1:8.
如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么S△OEF:S平行四边形ABCD=1:8. 分析 设平行四边形ABCD的面积是a,可求得△BCD的面积,又由OE∥AD交CD于点E,OF∥AB于点F,易得△DOE∽△DBC,△BOF∽△BDC,△CEF∽△CDB,然后由相似三角形面积比等于相似比的平方,求得答案.
解答 解:∵设平行四边形ABCD的面积是a,
∴S△BCD=$\frac{1}{2}$S?ABCD=$\frac{a}{2}$,OB=OD,
∵OE∥AD,OF∥AB,
∴△DOE∽△DBC,△BOF∽△BDC,
∴S△DOE=$\frac{1}{4}$S△BCD=$\frac{a}{8}$,S△BOF=$\frac{1}{4}$S△BCD=$\frac{a}{8}$,
∴DE=CE,BF=CF,
∴EF∥BD,EF=$\frac{1}{2}$BD,
∴△CEF∽△CDB,
∴S△CEF=$\frac{1}{4}$S△BCD=$\frac{a}{8}$,
∴S△EOF=$\frac{a}{2}$-$\frac{a}{8}$-$\frac{a}{8}$-$\frac{a}{8}$=$\frac{a}{8}$,
∴S△OEF:S平行四边形ABCD=$\frac{a}{8}$:a=1:8.
故答案为:1:8.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{45}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{5{a}^{2}}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点O是边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交△BCA的外角平分线于点F.
如图,在△ABC中,点O是边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交△BCA的外角平分线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com