某种小商品的销量y(件)与售价x(元)成一次函数关系.某商场以每件4元的单价进了一批这种商品,第一天以每件8元试销,结果售出60件,第二天以每件10元试销,结果售出50件.
(1)求销量y(件)与售价x(元)的函数关系式,并注明自变量x的取值范围.
(2)每件商品的售价定为多少元时,才能每天获得最大利润?每天的最大利润是多少元?
【答案】
分析:(1)首先根据题意,设y=kx+b,再将x=8,y=60及x=10,y=50代入,运用待定系数法求出销量y(件)与售价x(元)的函数关系式,然后根据售价x不低于成本及销量y为非负数,列出关于x的不等式组,解不等式组即可求出自变量x的取值范围;
(2)设每件商品的售价定为x元时,商场每天获得的利润为w元,根据利润=(售价-成本)×销售量,可列出w和x的关系式,然后根据函数的性质以及自变量的取值范围即可求解.
解答:解:(1)∵小商品的销量y(件)与售价x(元)成一次函数关系,
∴设y=kx+b,
由题意,得
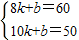
,
解得
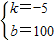
.
∴y=-5x+100.
∵

,
∴4≤x≤20;
(2)设每件商品的售价定为x元时,商场每天获得的利润为w元,由题意,得
w=(x-4)y=(x-4)(-5x+100)=-5(x-12)
2+320,
∵4≤x≤20,
∴当x=12时,w最大,此时w=320.
故每件商品的售价定为12元时,能使每天获得最大利润320元.
点评:本题主要考查运用待定系数法求一次函数的解析式及二次函数的应用,根据利润=(售价-成本)×销售量列出函数关系式,另外要熟练掌握二次函数求最值的方法.

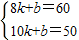 ,
,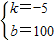 .
. ,
,
