
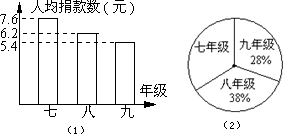
 18、如图(1),它是某中学“献爱心,资助贫困学生”自愿捐款活动中学生捐款情况的条形统计图,如图(2)是该校学生人数比例分布图,已知该校共有学生1450人.
18、如图(1),它是某中学“献爱心,资助贫困学生”自愿捐款活动中学生捐款情况的条形统计图,如图(2)是该校学生人数比例分布图,已知该校共有学生1450人.

科目:初中数学 来源: 题型:
 如图1是某公司的图标,它是由一个扇环形和圆组成,其设计方法如图2所示,ABCD是正方形,⊙O是该正方形的内切圆,E为切点,以B为圆心,分别以BA、BE为半径画扇形,得到如图所示的扇环形,图1中的圆与扇环的面积比为
如图1是某公司的图标,它是由一个扇环形和圆组成,其设计方法如图2所示,ABCD是正方形,⊙O是该正方形的内切圆,E为切点,以B为圆心,分别以BA、BE为半径画扇形,得到如图所示的扇环形,图1中的圆与扇环的面积比为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(73):3.4 弧长和扇形的面积,圆锥的侧面展开图(解析版) 题型:填空题
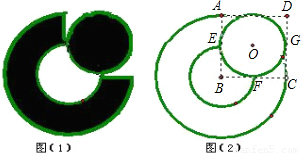
 如图1是某公司的图标,它是由一个扇环形和圆组成,其设计方法如图2所示,ABCD是正方形,⊙O是该正方形的内切圆,E为切点,以B为圆心,分别以BA、BE为半径画扇形,得到如图所示的扇环形,图1中的圆与扇环的面积比为 .
如图1是某公司的图标,它是由一个扇环形和圆组成,其设计方法如图2所示,ABCD是正方形,⊙O是该正方形的内切圆,E为切点,以B为圆心,分别以BA、BE为半径画扇形,得到如图所示的扇环形,图1中的圆与扇环的面积比为 .查看答案和解析>>
科目:初中数学 来源:第5章《中心对称图形(二)》中考题集(65):5.8 弧长及扇形的面积(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:第3章《圆的基本性质》中考题集(29):3.5 弧长及扇形的面积(解析版) 题型:填空题
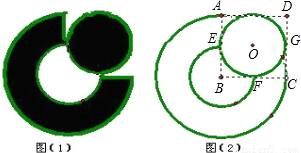
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com