
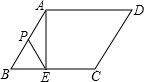
 如图,在菱形ABCD中,过A作AE⊥BC于E,P为AB上一动点,已知cosB=
如图,在菱形ABCD中,过A作AE⊥BC于E,P为AB上一动点,已知cosB= ,EC=8,则线段PE的长度最小值为________.
,EC=8,则线段PE的长度最小值为________.
 以及余弦的计算可得x=
以及余弦的计算可得x= ×(x+8),易求x,据图可知点E到线段AB的最小距离应该是过E作AB的垂线段的长度,再过E作EP⊥AB于P,在Rt△BPE中,再利用三角函数可求PE.
×(x+8),易求x,据图可知点E到线段AB的最小距离应该是过E作AB的垂线段的长度,再过E作EP⊥AB于P,在Rt△BPE中,再利用三角函数可求PE. 解:设BE=x,那么BC=x+8,
解:设BE=x,那么BC=x+8, ,AE⊥BC,
,AE⊥BC, ×(x+8),
×(x+8), •BE=
•BE= ×5=
×5= .
. .
. .
. 

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com