
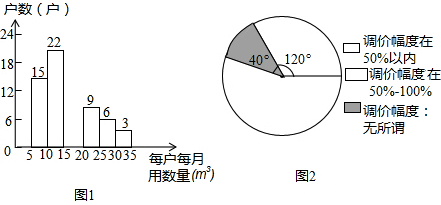
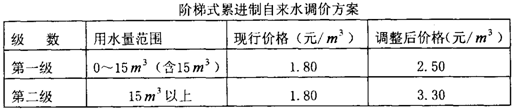
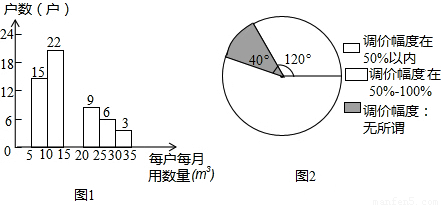
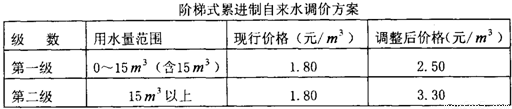
 ,
, =72,
=72,
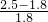 ×100%<50%;
×100%<50%;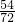 =75%,
=75%, ,可求出此次抽查的总人数,再根据各小组频数之和等于总人数求出居民用户每月的用水量在15m3~20m3之间的户数;
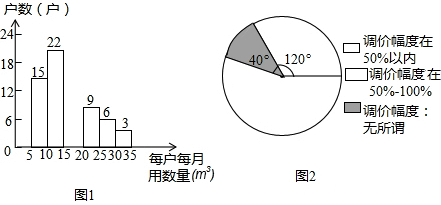
,可求出此次抽查的总人数,再根据各小组频数之和等于总人数求出居民用户每月的用水量在15m3~20m3之间的户数;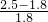 ×100%<50%;
×100%<50%;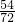 =75%,利用样本估计总体即可.
=75%,利用样本估计总体即可.

 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
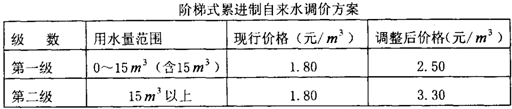
查看答案和解析>>
科目:初中数学 来源:重庆市期末题 题型:解答题
 个水龙头、
个水龙头、 个抽水马桶漏水.若一万个漏水的水龙头一个月能漏掉a立方米水;一万个漏水的马桶一个月漏掉b立方米水,则全市一个月仅这两项所造成的水流失量是多少?
个抽水马桶漏水.若一万个漏水的水龙头一个月能漏掉a立方米水;一万个漏水的马桶一个月漏掉b立方米水,则全市一个月仅这两项所造成的水流失量是多少?查看答案和解析>>
科目:初中数学 来源:2011年安徽省合肥市蜀山区中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com