
(1)把抛物线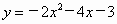 向右平移2个单位长度,再向上平移4个单位长度,求所得抛物线的关系式;
向右平移2个单位长度,再向上平移4个单位长度,求所得抛物线的关系式;
(2)把抛物线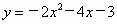 绕其顶点旋转180°后的关系式;
绕其顶点旋转180°后的关系式;
(3)抛物线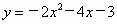 关于x轴对称的抛物线的关系式.
关于x轴对称的抛物线的关系式.
(4)抛物线 与
与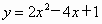 的形状相同,开口方向相反,顶点为(1,3),求该抛物线的关系式.
的形状相同,开口方向相反,顶点为(1,3),求该抛物线的关系式.
|
解: (1)法1:把抛物线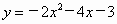 向右平移2个单位长度,再向上平移4个单位长度所得抛物线的关系式为 向右平移2个单位长度,再向上平移4个单位长度所得抛物线的关系式为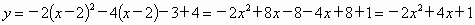
法 2:向右平移2个单位长度,再向上平移4个单位长度,顶点为(1,3) . ∴关系式为 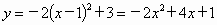 . .
(2) 抛物线∴二次项系数为 2.∴其关系式为: 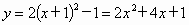 . .
(3) 抛物线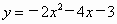 关于x轴对称的抛物线为 关于x轴对称的抛物线为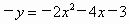 , ,
∴ 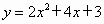 . .
(4) 抛物线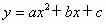 与 与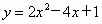 的开口方向相反,形状相同. 的开口方向相反,形状相同.
∴ a=-2,又顶点为(1,3),∴其关系式为 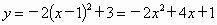 . . |
|
(1) 平移后开口方向,开口大小不变,形状不变,只是位置发生了变化;(2)旋转后开口方向相反,开口大小不变;二次项系数是原来的相反数,顶点不变; (3)关于x轴对称的点横坐标相等,纵坐标互为相反数; (4)可用顶点式求. |


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:关于![]() 的一元二次方程
的一元二次方程![]() (m为实数)
(m为实数)
1.若方程有两个不相等的实数根,求![]() 的取值范围;
的取值范围;
2.在(1)的条件下,求证:无论![]() 取何值,抛物线
取何值,抛物线![]() 总过
总过![]() 轴上的一个固定点;
轴上的一个固定点;
3.若![]() 是整数,且关于
是整数,且关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线![]() 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:关于![]() 的一元二次方程
的一元二次方程![]() (m为实数)
(m为实数)
(1)若方程有两个不相等的实数根,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:无论![]() 取何值,抛物线
取何值,抛物线![]() 总过
总过![]() 轴上的一个固定点;
轴上的一个固定点;
(3)若![]() 是整数,且关于
是整数,且关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线![]() 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:关于![]() 的一元二次方程
的一元二次方程![]() (m为实数)
(m为实数)
(1)若方程有两个不相等的实数根,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:无论![]() 取何值,抛物线
取何值,抛物线![]() 总过
总过![]() 轴上的一个固定点;
轴上的一个固定点;
(3)若![]() 是整数,且关于
是整数,且关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线![]() 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市启正中学九年级(上)月考数学试卷(10月份)(解析版) 题型:解答题
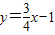 与抛物线
与抛物线 交于A、B两点(A在B的左侧),与y轴交于点C.
交于A、B两点(A在B的左侧),与y轴交于点C.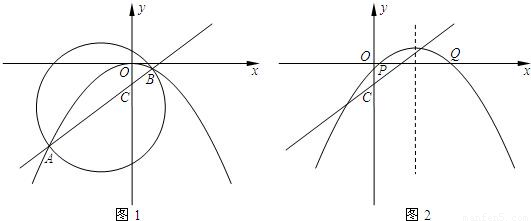
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com