练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．计算
    （1）$\sqrt{25}$-（π-3）0+$\root{3}{125}$；  
    （2）$\sqrt{{{（-2）}^2}}$+|1-$\sqrt{2}$|-$\sqrt{2}$．

    分析 （1）根据零指数幂、立方根、二次根式化简3个考点分别进行计算，然后根据实数的运算法则求得计算结果；
    （2）根据二次根式和绝对值分别进行计算即可得出答案．

    解答 解：（1）$\sqrt{25}$-（π-3）0+$\root{3}{125}$=5-1+5=9；  

    （2）$\sqrt{{{（-2）}^2}}$+|1-$\sqrt{2}$|-$\sqrt{2}$=2+$\sqrt{2}$-1-$\sqrt{2}$=1．

    点评 此题考查了实数的运算，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握零指数幂、二次根式、绝对值等考点的运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．如图所示，AD平分∠CAE，∠B=30°，∠CAD=65°，则∠ACD=80°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，某渔船在A处观测到灯塔M在它的北偏东48°方向上，这艘渔船以每小时28海里的速度向正东方向航行，半小时后到达B处，在B处观测到灯塔M在它的北偏东37°方向上．这艘渔船继续向正东航行多少海里，距离灯塔M最近？（参考数据：sin37°≈$\frac{3}{5}$，tan37°≈$\frac{3}{4}$，sin48°≈$\frac{7}{10}$，tan48°≈$\frac{11}{10}$，cos37°≈$\frac{4}{5}$，cos48°≈$\frac{7}{11}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

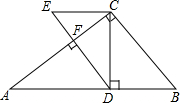    8．如图，在Rt△ACB中，∠ACB=90°，CD⊥AB于D，DF⊥AC于F，过C作CE∥AB交DF的延长线于点E，则下列结论中错误的是（　　）
    A．DE2=BD•ABB．S△CEF：S△ADF=BD2：AD2
    C．$\frac{BD}{CA}$=$\frac{CF}{AD}$D．$\frac{DF}{BC}$=$\frac{AF}{AB}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．数学老师在如图所示的黑板上写了一个关于x，y的方程，若$\left\{\begin{array}{l}{x=2}\\{y=-\frac{3}{2}}\end{array}\right.$和$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-4}\end{array}\right.$是该方程的两组解，则m，n的值分别为（　　）
    A．3，3B．2，2C．3，2D．2，3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）$\frac{x^2}{x-5}+\frac{25}{5-x}$
    （2）$\frac{1}{x-1}$-$\frac{x}{{{x^2}-1}}$
    （3）$\frac{x+2}{{{x^2}-2x}}-\frac{x-1}{{{x^2}-4x+4}}$
    （4）$\frac{a}{a+1}$+$\frac{a-1}{{a}^{2}-1}$
    （5）$\frac{x^2}{x-1}-x-1$
    （6）$\frac{{{x^2}-1}}{{{x^2}-2x+1}}$•$\frac{x-1}{{{x^2}+x}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知：如图，AD∥BC，∠A=∠C．
    （1）求证：AB∥CD；
    （2）若DE平分∠ADC交BC于E，∠A=40°，求∠DEC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．A县和B县分别有某种库存机器6台和12台，现决定支援C村10台，D村8台，已知从A县调运一台机器到C村和D村的运费分别是300元和500元；从B县调运一台机器到C村和D村的运费分别是400元和800元．
    （1）设A县运往C村机器x台，求总运费y关于x的函数关系式；
     （2）若要求总运费不超过9000元，共有几种调运方案？哪种调运方案运费最低？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．若a＞b，则下列各式中正确的是（　　）
    A．a-$\frac{1}{5}$＜b-$\frac{1}{5}$B．-4a＞-4bC．-2a+1＜-2b+1D．a2＞b2

    查看答案和解析>>

    同步练习册答案