
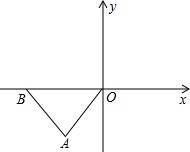
 如图,在下面直角坐标系中,已知A(-4,a),B(-8,0)
如图,在下面直角坐标系中,已知A(-4,a),B(-8,0)| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
数学课上,老师出示图和下面条件:

如图,在直角坐标平面内,O为坐标原点,A点坐标为(1,0),点B在x轴上且在点A的右侧,AB=OA.过点A和B作x轴的垂线,分别交二次函数y=x2的图像于点C和D.直线OC交BD于点M,直线CD交y轴于点H.记点C、D的横坐标分别为xC、xD,点H的纵坐标为yH.
同学发现两个结论:①S△CMD∶S梯形ABMC=2∶3;②数值相等关系:xC·xD=-yH.
(1)请你验证结论①和结论②成立;
(2)请你研究:如果将上述条件“A点坐标为(1,0)”改为“A点坐标为(t,0)(t>0)”,其他条件不变,结论①是否仍成立?(请说明理由)
(3)进一步研究:如果将上述条件“A点坐标为(1,0)”改为“A点坐标为(t,0)(t>0)”,又将条件“y=x2”改为“y=ax2(a>0)”,其他条件不变,那么xC、xD和yH有怎样的数值关系?(写出结果并说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
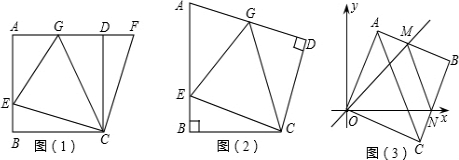
查看答案和解析>>
科目:初中数学 来源:2011年江苏省盐城市建湖县上冈实验初中中考数学模拟试卷(解析版) 题型:解答题
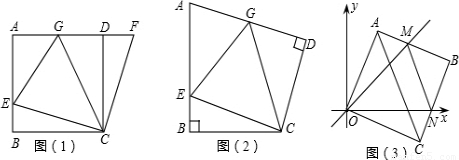
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com