练习册

  • 练习册
  • 试题
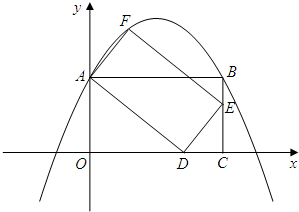    精英家教网 > 初中数学 > 题目详情

    如图，OA是⊙B的直径，OA=4，CD是⊙B的切线，D为切点，∠DOC=30°，则点C的坐标为________．

    （6，0）
    分析：连接BD，即可求得BC的长，进而求得OC的长，则坐标即可求得．
    解答：解：连接BD，
    ∵∠DOC=30°，
    ∴∠BDC=60°，
    ∴∠BCD=30°，
    ∴BC=2BD=4，
    ∴OC=OB+BC=6，
    故点C的坐标为（6，0）．
    故答案是：（6，0）．
    点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，火焰的光线穿过小孔O，在竖直的屏幕上形成倒立的实像，像的高度为1.5cm，OA=48cm，OC=16cm，则火焰的高度是
     
    cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，平面直角坐标系中，矩形ABCO的边OA在y正半轴上，OC在x正半轴上，点D是线段OC上一点，过点D作DE⊥AD交直线BC于点E，以A、D、E为顶点作矩形ADEF．
    （1）求证：△AOD∽△DCE；
    （2）若点A坐标为（0，4），点C坐标为（7，0）．
    ①当点D的坐标为（5，0）时，抛物线y=ax2+bx+c过A、F、B三点，求点F的坐标及a、b、c的值；
    ②若点D（k，0）是线段OC上任意一点，点F是否还在①中所求的抛物线上？如果在，请说明理由；如果不在，请举反例说明；
    （3）若点A的坐标是（0，m），点C的坐标是（n，0），当点D在线段OC上运动时，是否也存在一条抛物线，使得点F都落在该抛物线上？若存在，请直接用含m精英家教网、n的代数式表示该抛物线；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

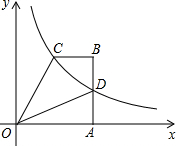    精英家教网直角梯形OABC中，BC∥OA，∠OAB=90°，OA=4，腰AB上有一点D，AD=2，四边形ODBC的面积为6，建立如图所示的直坐标系，反比例函数y=
    m
    x
    （x＞0）的图象恰好经过点C和点D，则CB与BD的比值是（　　）
    A、1
    B、
    4
    3
    C、
    6
    5
    D、
    8
    7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA．
    （1）求B点的坐标；
    （2）若抛物线y=-x2+bx+c经过点A、B．
    ①求抛物线的解析式及顶点坐标；
    ②将抛物线竖直向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：2006年初中数学总复习下册 题型：044

    如图所示是某学校田径体育场一部分的示意图，第一条跑道每圈为400 m．跑道分直道和弯道，直道为长相等的平行线段，弯道为同心的半圆形，弯道与直道相连接．已知直道BC的长为86.96 m，跑道的宽为1 m．(π＝3.14，结果精确到0.01 m)

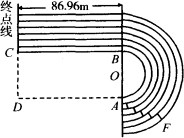
    (1)求第一条跑道的弯道部分()的半径；

    (2)求一圈中第二条跑道比第一条跑道长多少米？

    (3)若进行200 m比赛，求第六道的起点F与圆心O的连线FO与OA的夹角∠FOA的度数．

    查看答案和解析>>

    同步练习册答案