
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:设计九年级上数学人教版 人教版 题型:013
已知弧AB、弧CD是同圆的两条弧,且弧AB的长度是弧CD的2倍,则
A.AB=2CD
B.AB<2CD
C.AB>2CD
D.AB与2CD不能比较大小
查看答案和解析>>
科目:初中数学 来源:2012届江苏省大丰市九年级第一次调研考试数学试卷(带解析) 题型:解答题
已知:如图,M是线段BC的中点,BC=4,分别以MB、MC为边在线段BC的同侧作等边△BAM、等边△MCD,连接AD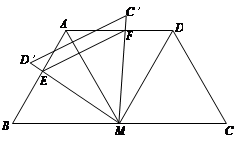
【小题1】求证:四边形ABCD是等腰梯形
【小题2】将△MDC绕点M逆时针方向旋转α(60º<α<120º),得到△MD´C´,MD´交AB于点E,MC´交AD于点F,连接EF.
①求证:EF∥D´C´;
②△AEF的周长是否存在最小值?如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省大丰市九年级第一次调研考试数学试卷(解析版) 题型:解答题
已知:如图,M是线段BC的中点,BC=4,分别以MB、MC为边在线段BC的同侧作等边△BAM、等边△MCD,连接AD

1.求证:四边形ABCD是等腰梯形
2.将△MDC绕点M逆时针方向旋转α(60º<α<120º),得到△MD´C´,MD´交AB于点E,MC´交AD于点F,连接EF.
①求证:EF∥D´C´;
②△AEF的周长是否存在最小值?如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com