
���� ��1�����ݻ�Ԫ�����ɵô𰸣�
��2�����ݷ�ʽ�ļӼ����ɵã�$\frac{x-1}{x+2}$-$\frac{x+2}{x-1}$=0�����ݻ�Ԫ�����ɵô𰸣�
��� �⣺��1��y-$\frac{4}{y}$=0��
��2��ԭ���̻�Ϊ��$\frac{x-1}{x+2}$-$\frac{x+2}{x-1}$=0��
��y=$\frac{x-1}{x+2}$����ԭ���̻�Ϊ��y-$\frac{1}{y}$=0��
��������ͬʱ����y�ã�y2-1=0����ã�y=��1��
�����飺y=��1���Ƿ���y-$\frac{1}{y}$=0�Ľ⣮
��y=1ʱ��$\frac{x-1}{x+2}$=1���÷����⣻
��y=-1ʱ��$\frac{x-1}{x+2}$=-1����ã�x=-$\frac{1}{2}$��
�����飺x=-$\frac{1}{2}$��ԭ��ʽ���̵Ľ⣬
��ԭ��ʽ���̵Ľ�Ϊx=-$\frac{1}{2}$��
���� ���⿼���˽��ʽ���̣����û�Ԫ���ǽ���ؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ϵ�̫������������ | |
| B�� | ���ӻ��������ڲ��������籭 | |
| C�� | ������һö�ʵؾ��ȵ����ӣ������ĵ�����ż�� | |
| D�� | С���˴���ĩ������ѧ����100�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
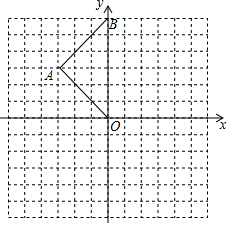 ��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��OAB�Ķ�����ڸ���ϣ�
��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��OAB�Ķ�����ڸ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
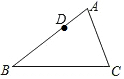 �ڡ�ABC�У�AB=6��AC=4��D���߶�AB�ϵ�һ�㣬��AD=2����E���߶�AC�ϵ�һ�㣬�ҡ�ADE���ABC���ƣ���AE=$\frac{4}{3}$��3��
�ڡ�ABC�У�AB=6��AC=4��D���߶�AB�ϵ�һ�㣬��AD=2����E���߶�AC�ϵ�һ�㣬�ҡ�ADE���ABC���ƣ���AE=$\frac{4}{3}$��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ⲻ��ʽ�飺$\left\{\begin{array}{l}{x-3��0����}\\{\frac{3x+1}{12}��\frac{2x-1}{3}����}\end{array}\right.$���Ѳ���ʽ��Ľ⼯��ʾ�������ϣ�
�ⲻ��ʽ�飺$\left\{\begin{array}{l}{x-3��0����}\\{\frac{3x+1}{12}��\frac{2x-1}{3}����}\end{array}\right.$���Ѳ���ʽ��Ľ⼯��ʾ�������ϣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com