解:(1)

,
=3-4-2,
=-3;
(2)a
2-4(a-b)
2,
=(a+2a-2b)(a-2a+2b),
=(3a-2b)(-a+2b);
(3)
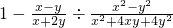
,
=1-
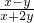
•

,
=1-

,
=-

;
(4)(3x+2)(3x-2)-5x(x+1)-(2x-1)
2,
=9x
2-4-5x
2-5x-4x
2+4x-1,
=-x-5.
当x=

时,原式=-x-5=

-5=-4

.
(5)方程两边同乘以x(x-1),得
6x+3(x-1)=x+5,
解得x=1,
将x=1代入x(x-1)=0,所以原方程无解.
分析:(1)先化简,再合并即可;
(2)运用平方差公式分解因式;
(3)这是个分式除法与减法混合运算题,运算顺序是先做除法,要注意先把除法运算转化为乘法运算,而做乘法运算时要注意先把分子、分母能因式分解的先分解,然后约分,做减法时,要确定最简公分母进行通分;
(4)先把分式化简,再将未知数的值代入求解;
(5)观察可得最简公分母是x(x-1),方程两边乘以最简公分母,可以把分式方程化为整式方程,再求解.
点评:本题考查了解分式方程.解分式方程首先在方程两边乘以最简公分母,化为整式方程再求解,注意一定要检验.

 .
.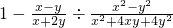 .
. .
.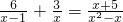
 ,
,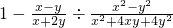 ,
,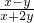 •
• ,
, ,
, ;
; 时,原式=-x-5=
时,原式=-x-5= -5=-4
-5=-4 .
.

