
分析 设累计购物x元,分别表示出在甲乙两商场的花费,列不等式,分情况讨论,求出最合适的消费方案.
解答 解:(1)当累计购物不超过50元时,在甲乙两商场的花费一样;
②当累计消费超过50元而不超过100元时,在乙商场享受优惠,在甲商场不享受优惠,因此应该到乙商场购买;
③当累计消费超过100元时,设累计消费x元(x>100),
甲商场消费为:100+(x-100)×0.9元,
在乙商场消费为:50+(x-50)×0.95元,
当100+(x-100)×0.9>50+(x-50)×0.95,解得:x<150,
当100+(x-100)×0.9<50+(x-50)×0.95,解得:x>150,
当100+(x-100)×0.9=50+(x-50)×0.95,解得:x=150,
综上所述,当累计消费大于100元少于150元时,在乙商店花费少;
当累计消费大于150元时,在甲商店花费少;
当累计消费等于150元或不超过50元时,在甲乙商场花费一样.
点评 本题考查了一元一次不等式的应用,解答本题的关键是读懂题意,将现实生活中的事件与数学思想联系起来,列出不等式关系式即可求解.注意此题分类讨论的数学思想.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{a+2b}$ | B. | $\frac{a}{-a-2b}$ | C. | $-\frac{a}{a+2b}$ | D. | $-\frac{a}{a-2b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
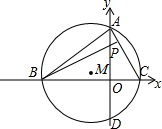 如图,在平面直角坐标系中,A(0,6),P(0,4),点C为x轴正半轴上任一点,BP⊥AC交x轴于B点,△ABC内接于⊙M交y轴负半轴于D点.
如图,在平面直角坐标系中,A(0,6),P(0,4),点C为x轴正半轴上任一点,BP⊥AC交x轴于B点,△ABC内接于⊙M交y轴负半轴于D点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.
如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC2的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com