
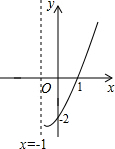
 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2-4ac>0;③a-b+c=0;④2a-b=0.正确的有( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2-4ac>0;③a-b+c=0;④2a-b=0.正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 此题可利用排除法进行判断,根据二次函数图象的开口方向确定a>0,再根据对称轴在y轴左,可确定a与b同号,然后再根据二次函数与y轴的交点可以确定c<0,进而可以判断出①的正误,然后再根据抛物线与x轴的交点个数可以判断出②的正误,再根据x=-1时,结合图象可得到y的正负,进而可以判断出③的正误,由对称轴x=-$\frac{b}{2a}$>-1,可得出$\frac{b}{2a}$<1,得出2a-b>0,进而可以判断出④的正误,进而得到答案.
解答 解:∵抛物线开口向上,
∴a>0,
∵对称轴在y轴左侧,
∴a与b同号,
∴b>0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc<0,故①正确;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,故②正确;
当x=-1时,a-b+c<0,故③正确;
∵抛物线的对称轴x=-$\frac{b}{2a}$>-1,
∴$\frac{b}{2a}$<1,
∴b<2a,
∴2a-b>0,故④错误;
故选:C.
点评 此题主要考查了二次函数图象与系数的关系,关键是掌握二次函数y=ax2+bx+c(a≠0),
①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口.
②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)
③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 若已知两点之间的所有连线中,线段最短,那么你能否试着解决下面的问题呢?
若已知两点之间的所有连线中,线段最短,那么你能否试着解决下面的问题呢?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小鹏的手中有一根长为40cm的铜丝,他想用这根铜丝分段围成一个面积为50cm2的如图所示的“日“字的矩形钢丝框,求该矩形钢丝框的长.设该矩形铜丝框的长为xcm,根据题意,可列方程为( )
小鹏的手中有一根长为40cm的铜丝,他想用这根铜丝分段围成一个面积为50cm2的如图所示的“日“字的矩形钢丝框,求该矩形钢丝框的长.设该矩形铜丝框的长为xcm,根据题意,可列方程为( )| A. | x($\frac{40-3x}{2}$)=50 | B. | x($\frac{40-2x}{3}$)=50 | C. | x(40-3x)=50 | D. | x(40-2x)=50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com