
如图3416,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴与B,C两点(点B在点C的左侧),已知A点坐标为(0,-5).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴与⊙C的位置关系,并给出证明;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形.若存在,求点P的坐标;若不存在,请说明理由.
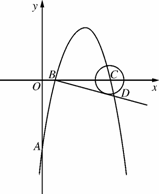
图3416
解:(1)设此抛物线的解析式为y=a(x-3)2+4,
此抛物线过点A(0,-5),
∴-5=a(0-3)2+4,∴a=-1.
∴抛物线的解析式为y=-(x-3)2+4,
即y=-x2+6x-5.
(2)抛物线的对称轴与⊙C相离.
证明:令y=0,即-x2+6x-5=0,得x=1或x=5,
∴B(1,0),C(5,0).
设切点为E,连接CE,
由题意,得,Rt△ABO∽Rt△BCE.
∴ =
= ,即
,即 =
= ,
,
解得CE= .
.
∵以点C为圆心的圆与直线BD相切,⊙C的半径为r=d= .
.
又点C到抛物线对称轴的距离为5-3=2,而2> .
.
则此时抛物线的对称轴与⊙C相离.
(3)假设存在满足条件的点P(xp,yp),
∵A(0,-5),C(5,0),
∴AC2=50,
AP2=(xp-0)2+(yp+5)2=x +y
+y +10yp+25,CP2=(xp-5)2+(yp-0)2=x
+10yp+25,CP2=(xp-5)2+(yp-0)2=x +y
+y -10xp+25.
-10xp+25.
①当∠A=90°时,在Rt△CAP中,
由勾股定理,得AC2+AP2=CP2,
∴50+x +y
+y +10yp+25=x
+10yp+25=x +y
+y -10xp+25,
-10xp+25,
整理,得xp+yp+5=0.
∵点P(xp,yp)在抛物线y=-x2+6x-5上,
∴yp=-x +6xp-5.
+6xp-5.
∴xp+(-x +6xp-5)+5=0,
+6xp-5)+5=0,
解得xp=7或xp=0,∴yp=-12或yp=-5.
∴点P为(7,-12)或(0,-5)(舍去).
②当∠C=90°时,在Rt△ACP中,
由勾股定理,得AC2+CP2=AP2,
∴50+x +y
+y -10xp+25=x
-10xp+25=x +y
+y +10yp+25,
+10yp+25,
整理,得xp+yp-5=0.
∵点P(xp,yp)在抛物线y=-x2+6x-5上,
∴yp=-x +6xp-5,
+6xp-5,
∴xp+(-x +6xp-5)-5=0,
+6xp-5)-5=0,
解得xp=2或xp=5,∴yp=3或yp=0.
∴点P为(2,3)或(5,0)(舍去)
综上所述,满足条件的点P的坐标为(7,-12)或(2,3).


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
如图3312,已知一次函数y1=kx+b与反比例函数y2=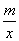 的图象交于A(2,4),B(-4,n)两点.
的图象交于A(2,4),B(-4,n)两点.
(1)分别求出y1和y2的解析式;
(2)写出当y1=y2时,x的值;
(3)写出当y1>y2时,x的取值范围.
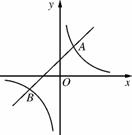
图3312
查看答案和解析>>
科目:初中数学 来源: 题型:
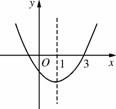
如图3411,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
A.abc<0 B.2a+b<0 C.a-b+c<0 D.4ac-b2<0
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A.x1=1,x2=-1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
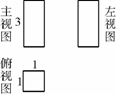
图6219是一个几何体的三视图,根据图中提供的数据(单位:cm),可求得这个几何体的体积为( )
A.2 cm3 B.3 cm3 C.6 cm3 D.8 cm3
查看答案和解析>>
科目:初中数学 来源: 题型:
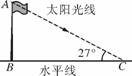
如图J46,在“测量旗杆的高度”的数学课题学习中,某学习小组测得太阳光线与水平面的夹角为27°,此时旗杆在水平地面上的影子长度为24米,则旗杆的高度约为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com