
如图,在钝角△ABC中,AD⊥BC,垂足为D点,且AD与DC的长度为x2-7x+12=0的两个根(AD<DC),⊙O为△ABC的外接圆,如果BD的长为6,求△ABC的外接圆⊙O的面积.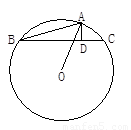
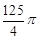
【解析】
试题分析:过O作OE⊥AB于E,连接OB, 可得∠AOE=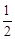 ∠AOB,AE=
∠AOB,AE=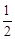 AB,即可得到∠C=
AB,即可得到∠C=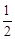 ∠AOB=∠AOE,解方程x2-7x+12=0可得DC=4,AD=3,根据勾股定理可得AB、AE的长,证得Rt△ADC∽Rt△AEO,根据相似三角形的性质可得AO的长,即可求得结果.
∠AOB=∠AOE,解方程x2-7x+12=0可得DC=4,AD=3,根据勾股定理可得AB、AE的长,证得Rt△ADC∽Rt△AEO,根据相似三角形的性质可得AO的长,即可求得结果.
过O作OE⊥AB于E,连接OB,
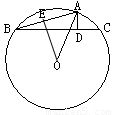
则∠AOE=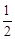 ∠AOB,AE=
∠AOB,AE=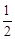 AB,
AB,
∴∠C=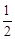 ∠AOB="∠AOE."
∠AOB="∠AOE."
解方程x2-7x+12=0可得DC=4,AD=3,
故AB= ,AE=
,AE= ,
,
证得Rt△ADC∽Rt△AEO,故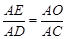 ,
,
又AC=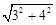 ="5," AD=3,AE=
="5," AD=3,AE= ,
,
故AO=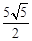 ,
,
从而S⊙O=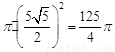 .
.
考点:垂径定理,解一元二次方程,勾股定理,相似三角形的判定和性质
点评:本题综合性强,知识点较多,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
 26、如图,在钝角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE.有下列结论:①∠1=∠2;②∠1=∠3;③∠B=∠C;④∠B=∠3.其中一定正确的结论有( )个.
26、如图,在钝角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE.有下列结论:①∠1=∠2;②∠1=∠3;③∠B=∠C;④∠B=∠3.其中一定正确的结论有( )个.查看答案和解析>>
科目:初中数学 来源: 题型:
 ,连接AO、BE、DC.
,连接AO、BE、DC.查看答案和解析>>
科目:初中数学 来源: 题型:
 23、如图,在钝角△ABC中,AB=AC,以BC为直径作⊙O,⊙O与BA、CA的延长线分别交于E、D两点,连接AO、DB、EC,试写出图中三对全等三角形,并对其中一对全等三角形进行证明.
23、如图,在钝角△ABC中,AB=AC,以BC为直径作⊙O,⊙O与BA、CA的延长线分别交于E、D两点,连接AO、DB、EC,试写出图中三对全等三角形,并对其中一对全等三角形进行证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com