
(本小题10分)在等腰梯形ABCD中,AD∥BC,且AD=2,以CD为直径作⊙
O1,交BC于点E,过点E作EF⊥AB于F,建立如图12所示的平面直角坐标系,已知A,
B两点的坐标分别为A(0,2![]() ),B(-2,0).
),B(-2,0).
(1)求C,D两点的坐标.
(2)求证:EF为⊙O1的切线.
(3)探究:如图13,线段CD上是否存在点P,使得线段PC的长度与P点到y轴的距离相等?如果存在,请找出P点的坐标;如果不存在,请说明理由.
(1)连结DE,∵CD是⊙O1的直径,
∴DE⊥BC,
∴四边形ADEO为矩形.
∴OE=AD=2,DE=AO=2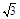 .
.
在等腰梯形ABCD中,DC=AB.
∴CE=BO=2,CO=4.
∴C(4,0),D(2,2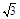 ).
).
(2)连结O1E,在⊙O1中,O1E=O1C,
∠O1EC=∠O1CE,
在等腰梯形ABCD中,∠ABC=∠DCB.
∴O1E∥AB,
又∵EF⊥AB,
∴O1E⊥EF.
∵E在AB上,
∴EF为⊙O1的切线
(3)解法一:存在满足条件的点P.
如右图,过P作PM⊥y轴于M,作PN⊥x轴于N,依题意得PC=PM,
在矩形OMPN中,ON=PM,
设ON=x,则PM=PC=x,CN=4-x,
tan∠ABO=![]() .
.
∴∠ABO=60°,
∴∠PCN=∠ABO =60°.
在Rt△PCN中,
cos∠PCN =![]() ,
,
即![]() ,
,
∴x= .
.
∴PN=CN·tan∠PCN=(4-![]() )·
)·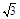 =
=![]() .
.
∴满足条件的P点的坐标为(![]() ,
,![]() ).
).
解法二:存在满足条件的点P,
如右图,在Rt△AOB中,AB=![]() .
.
过P作PM⊥y轴于M,作PN⊥x轴于N,依题意得PC=PM,
在矩形OMPN中,ON=PM,
设ON=x,则PM=PC=x,CN=4-x,
∵∠PCN=∠ABO,∠PCN=∠AOB=90°.
∴△PNC∽△AOB,
∴![]() ,即
,即![]() .
.
解得x= .
.
又由△PNC∽△AOB,得
![]() ,
,
∴PN= ![]() .
.
∴满足条件的P点的坐标为(![]() ,
,![]() ).
).
解析:略


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
| 13 |
| 13 |
| 13 |

查看答案和解析>>
科目:初中数学 来源: 题型:
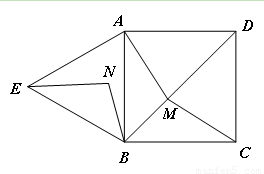
(本小题10分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(Ⅰ) 求证:△AMB≌△ENB;
(Ⅱ) ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(Ⅲ) 当AM+BM+CM的最小值为时,求正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
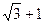 时,求正方形的边长.
时,求正方形的边长. 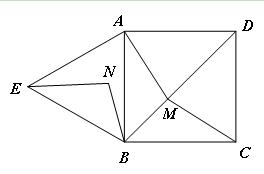
查看答案和解析>>
科目:初中数学 来源:2011年滨海新区大港初中毕业生学业考试第一次模拟试卷数学 题型:解答题
(本小题10分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(Ⅰ)求证:△AMB≌△ENB;
(Ⅱ)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(Ⅲ)当AM+BM+CM的最小值为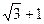 时,求正方形的边长.
时,求正方形的边长. 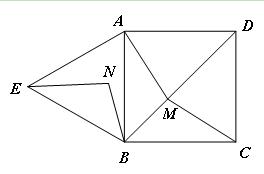
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖北十堰卷)数学 题型:解答题
(本小题10分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(Ⅰ) 求证:△AMB≌△ENB;
(Ⅱ) ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(Ⅲ) 当AM+BM+CM的最小值为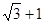 时,求正方形的边长.
时,求正方形的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com