
在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段
![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() .线段
.线段![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() ,连接AD.
,连接AD.
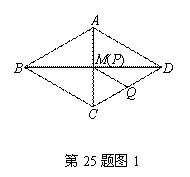
(1) 若![]() 且点
且点![]() 与点
与点![]() 重合(如图1),求证四边形ABCD为菱形;
重合(如图1),求证四边形ABCD为菱形;
(2) 在图2中,点![]() 不与点
不与点![]() 重合,猜想
重合,猜想![]() 的大小(用含
的大小(用含![]() 的代数式表示),并加以证明;
的代数式表示),并加以证明;
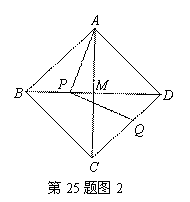
 (3) 对于适当大小的
(3) 对于适当大小的![]() ,当点
,当点![]() 在线段
在线段![]() 上运动到某一位置(不与点
上运动到某一位置(不与点![]() ,
,![]() 重合)时,能使得线段
重合)时,能使得线段![]() 的延长线与射线
的延长线与射线![]() 交于点
交于点![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的范围.
的范围.
科目:初中数学 来源: 题型:
已知:在梯形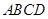 中,
中,![]() 点
点![]() 是
是![]() 的中点,
的中点,![]() 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段![]() 和
和![]() 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.

(1)求证:△BMP∽△CPQ
(2)设PC=![]() ,MQ=
,MQ=![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在(2)中,当![]() 取最小值时,判断
取最小值时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届北京第四十一中学九年级上期期中数学试卷(带解析) 题型:解答题
已知:在梯形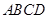 中,
中,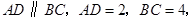 点
点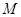 是
是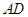 的中点,
的中点,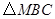 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段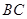 和
和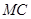 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.
(1)求证:△BMP∽△CPQ
(2)设PC=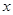 ,MQ=
,MQ=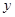 求
求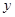 与
与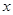 的函数关系式;
的函数关系式;
(3)在(2)中,当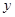 取最小值时,判断
取最小值时,判断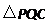 的形状,并说明理由.
的形状,并说明理由.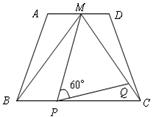
查看答案和解析>>
科目:初中数学 来源:2011-2012学年九年级第二学期测试数学卷 题型:解答题
已知:在梯形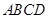 中,
中,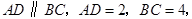 点
点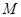 是
是 的中点,
的中点,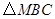 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段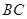 和
和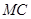 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.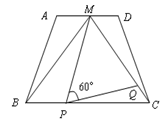
(1)求证:△BMP∽△CPQ
(2)设PC=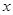 ,MQ=
,MQ=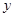 求
求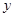 与
与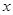 的函数关系式;
的函数关系式;
(3)在(2)中,当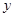 取最小值时,判断
取最小值时,判断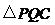 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届九年级第二学期测试数学卷 题型:解答题
已知:在梯形 中,
中, 点
点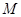 是
是 的中点,
的中点, 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段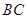 和
和 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.
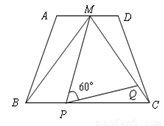
(1)求证:△BMP∽△CPQ
(2)设PC=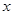 ,MQ=
,MQ= 求
求 与
与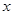 的函数关系式;
的函数关系式;
(3)在(2)中,当 取最小值时,判断
取最小值时,判断 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com