
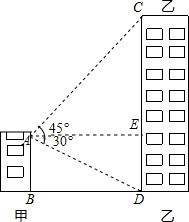
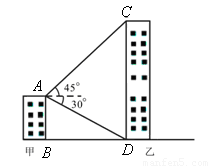
 如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为________米.
如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为________米. )
)
 ,
, =10
=10 米,
米, )米,
)米, ).
).

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,甲乙两幢楼之间的距离CD等于45米,现在要测乙楼的高BC,(BC⊥CD),所选观察点A在甲楼一窗口处,AD∥BC.从A处测得乙楼顶端B的仰角为45°,底部C的俯角为30°,求乙楼的高度 (取
如图,甲乙两幢楼之间的距离CD等于45米,现在要测乙楼的高BC,(BC⊥CD),所选观察点A在甲楼一窗口处,AD∥BC.从A处测得乙楼顶端B的仰角为45°,底部C的俯角为30°,求乙楼的高度 (取| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
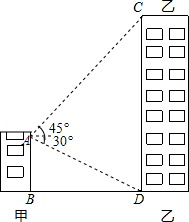 (2013•西宁)如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为
(2013•西宁)如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012届浙江省嵊州市初中毕业生学业评价调测数学试卷(带解析) 题型:解答题
如图,甲乙两幢楼之间的距离CD等于45米,现在要测乙楼的高BC,(BC⊥CD),所选观察点A在甲楼一窗口处,AD∥BC.从A处测得乙楼顶端B的仰角为45°,底部C的俯角为30°,求乙楼的高度 (取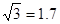 ,结果精确到1米) .
,结果精确到1米) .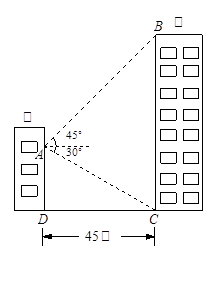
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:填空题
如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为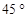 ,测得乙楼底部D处的俯角为
,测得乙楼底部D处的俯角为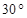 ,则乙楼的高度为 米.
,则乙楼的高度为 米.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省嵊州市初中毕业生学业评价调测数学试卷(解析版) 题型:解答题
如图,甲乙两幢楼之间的距离CD等于45米,现在要测乙楼的高BC,(BC⊥CD),所选观察点A在甲楼一窗口处,AD∥BC.从A处测得乙楼顶端B的仰角为45°,底部C的俯角为30°,求乙楼的高度 (取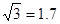 ,结果精确到1米)
.
,结果精确到1米)
.
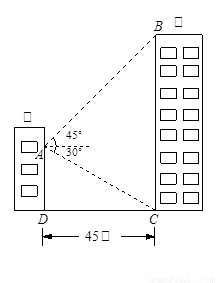
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com