
分析 (1)分两种情况进行讨论:①当∠A为锐角时,如图1所示;②当∠A为钝角时,如图2所示,分别根据角的和差关系求得y关于x的函数表达式,并写出自变量的取值范围即可;
(2)当x=60°时,由(1)可得,y=180°-2×60°=60°,得出∠EDF=60°,再根据Rt△BCE中,DE=$\frac{1}{2}$BC,Rt△BCF中,DF=$\frac{1}{2}$BC,可得DE=DF,据此判定△DEF的形状为等边三角形;
(3)分两种情况进行讨论:①当∠A为锐角时,如图1所示;②当∠A为钝角时,如图2所示,分别根据△DEF为等腰直角三角形,且DE=DF,得出∠EDF为直角,即y=90,分别运用(1)中的函数解析式即可求得x的值.
解答 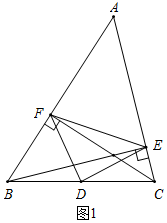 解:(1)①当∠A为锐角时,如图1所示,
解:(1)①当∠A为锐角时,如图1所示,
∵BE⊥AC于E,CF⊥AB于F,BD=DC,
∴Rt△BCE中,DE=$\frac{1}{2}$BC=CD,
Rt△BCF中,DF=$\frac{1}{2}$BC=BD,
∴∠BDE=2∠DCE,∠CDF=2∠DBF,
又∵∠BDE+∠CDF-∠EDF=180°,
∴2∠DCE+2∠DBF-∠EDF=180°,
即2(∠DCE+∠DBF)-∠EDF=180°,
∴2(180°-∠A)-∠EDF=180°,
又∵∠BAC=x,∠EDF=y,
∴2(180-x)-y=180,
∴y=2(180-x)-180,
即y=180-2x(0<x<90);
②当∠A为钝角时,如图2所示,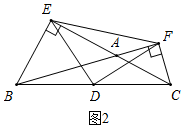
∵BE⊥AC于E,CF⊥AB于F,BD=DC,
∴Rt△BCE中,DE=$\frac{1}{2}$BC=CD,
Rt△BCF中,DF=$\frac{1}{2}$BC=BD,
∴∠BDE=2∠DCE,∠CDF=2∠DBF,
又∵∠BDE+∠CDF+∠EDF=180°,
∴2∠DCE+2∠DBF+∠EDF=180°,
即2(∠DCE+∠DBF)+∠EDF=180°,
∴2(180°-∠A)+∠EDF=180°,
又∵∠BAC=x,∠EDF=y,
∴2(180-x)+y=180,
∴y=180-2(180-x),
即y=2x-180(90<x<180);
综上所述,y关于x的函数表达式为y=$\left\{\begin{array}{l}{180-2x(0<x<90)}\\{2x-180(90<x<180)}\end{array}\right.$;
(2)当x=60°时,由(1)可得,y=180°-2×60°=60°,
即∠EDF=60°,
又∵Rt△BCE中,DE=$\frac{1}{2}$BC,
Rt△BCF中,DF=$\frac{1}{2}$BC,
∴DE=DF,
∴△DEF的形状为等边三角形;
(3)①如图1,∵△DEF为等腰直角三角形,且DE=DF,
∴∠EDF为直角,
即y=90,
此时,90=180-2x,
解得x=45,
故x的值为45;
②如图2,∵△DEF为等腰直角三角形,且DE=DF,
∴∠EDF为直角,
即y=90,
此时,90=2x-180,
解得x=135,
故x的值为135;
综上所述,若△DEF为等腰直角三角形,x的值为45或135.
点评 本题属于三角形综合题,主要考查了直角三角形的性质,等腰三角形的性质以及等边三角形的判定的综合应用,解决问题的关键是画出相应的图形,运用分类讨论思想,根据角的和差关系进行求解.


科目:初中数学 来源: 题型:选择题
| A. | 单项式$\frac{3}{2}π{x^2}y$的系数是$\frac{3}{2}$ | |
| B. | 若AB=BC,则点B是线段AC的中点 | |
| C. | 3和5是同类项 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
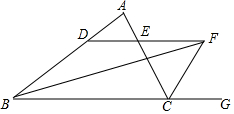 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长.
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
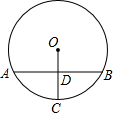 如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2$\sqrt{3}$,点E在⊙O上,∠EOA=30°,则△EOC的面积为1或2.
如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2$\sqrt{3}$,点E在⊙O上,∠EOA=30°,则△EOC的面积为1或2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读下面材料:下面是“作角的平分线”的尺规作图过程.
阅读下面材料:下面是“作角的平分线”的尺规作图过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com