
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 比赛日期 | 2012-8-4 | 2013-5-21 | 2014-9-28 | 2015-5-20 | 2015-5-31 |
| 比赛地点 | 英国伦敦 | 中国北京 | 韩国仁川 | 中国北京 | 美国尤金 |
| 成绩(秒) | 10.19 | 10.06 | 10.10 | 10.06 | 9.99 |
| A. | 10.06秒,10.06秒 | B. | 10.10秒,10.06秒 | C. | 10.06秒,10.08秒 | D. | 10.08秒,10.06秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
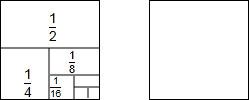 (1)请用多种方法计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.
(1)请用多种方法计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
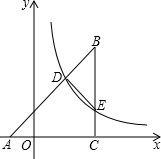 如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2$\sqrt{2}$,反比例函数y=$\frac{3}{x}$(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为($\frac{3}{2}\sqrt{2}$,$\sqrt{2}$).
如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2$\sqrt{2}$,反比例函数y=$\frac{3}{x}$(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为($\frac{3}{2}\sqrt{2}$,$\sqrt{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com