
某学生站在公园湖边的M处,测得湖心亭A位于北偏东30°方向上,又测得游船码头B位于南偏东60°方向上.现有一艘游船从湖心亭A 处沿正南方向航行返回游船码头,已知M处与AB的距离MN=0.7千米,求湖心亭与游船码头B的距离(精确到0.1千米).
1.6千米
【解析】
试题分析:先在Rt△AMN中根据含30° 的直角三角形的性质求得AM的长,再在Rt△AMB中,根据∠A的余弦函数即可求得结果.
如图,由已知得∠AMB=90°,∠A=30°,MN=0.7千米
在Rt△AMN中,∠A=30°,∠ANM=90°,MN=0.7千米
∴AM=2MN=1.4(千米).
在Rt△AMB中,∠A=30°,∠AMB=90°,AM=1.4千米
∴AB=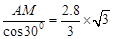 ≈1.6(千米)
≈1.6(千米)
即湖心亭A到游船码头B的距离约为1.6千米.
考点:解直角三角形的应用
点评:直角三角形的判定和性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.


科目:初中数学 来源:活学巧练 九年级数学 下 题型:044
某学生站在公园湖边的M处,测得湖心亭A位于北偏东![]() 方向上,又测得游船码头B位于南偏东
方向上,又测得游船码头B位于南偏东![]() 方向上.现有一艘游船从湖心亭A处沿正南方向航行返回游船码头,已知M处与AB的距离MN=0.7千米,求湖心亭与游船码头B的距离(精确到0.1千米).
方向上.现有一艘游船从湖心亭A处沿正南方向航行返回游船码头,已知M处与AB的距离MN=0.7千米,求湖心亭与游船码头B的距离(精确到0.1千米).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com