1
分析:解不等式a
2-a-2>0得到a>2或a<-1,然后把a
2+b
2+c
2+42<4a+4b+12c用配方法得到(a-2)
2+(b-2)
2+(c-6)
2<2,根据a,b,c是自然数,确定a=3,b=2,c=6,把a,b,c的值代入代数式求出代数式的值.
解答:∵a
2-a-2>0,(a-2)(a+1)>0,∴a>2或a<-1.
a
2+b
2+c
2+42-4a-4b-12c<0
配方得:(a-2)
2+(b-2)
2+(c-6)
2<2,
∵a,b,c是自然数,∴a=3,b=2,c=6,
∴

+

+

=

+

+

=
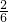
+
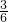
+

=1.
故答案是:1.
点评:本题考查的是解一元二次不等式,通过解不等式求出a,b,c的值,然后代入代数式求出代数式的值.

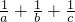 的值是 ________.
的值是 ________. +
+ +
+ =
= +
+ +
+ =
=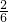 +
+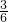 +
+ =1.
=1.
