
| A. | 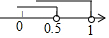 | B. | 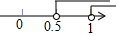 | C. | 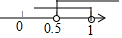 | D. | 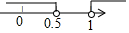 |
分析 先确定出点M在第三象限,然后根据第三象限内点的横坐标与纵坐标都是负数列出不等式组,然后求解得到m的取值范围,从而得解.
解答 解:∵点M(1-2m,m-1)关于原点的对称点在第一象限,
∴点M(1-2m,m-1)在第三象限,
∴$\left\{\begin{array}{l}{1-2m<0①}\\{m-1<0②}\end{array}\right.$,
解不等式①得,m>$\frac{1}{2}$,
解不等式②得,m<1,
所以,m的取值范围是$\frac{1}{2}$<m<1,
在数轴上表示如下: .
.
故选C.
点评 本题主要考查了平面直角坐标系中,各象限内点的坐标的符号的确定方法,以及关于原点对称的两点坐标之间的关系以及一元一次不等式组的解法.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
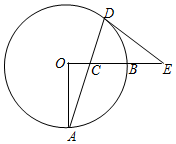 如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
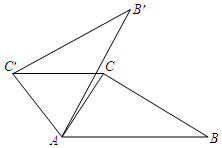 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
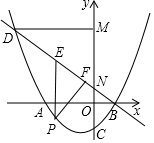 如图,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,-$\frac{5}{2}$).直线y=mx+$\frac{3}{2}$过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.
如图,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,-$\frac{5}{2}$).直线y=mx+$\frac{3}{2}$过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.
如图,在等腰△ABC中,AB=AC=5,半径为1的⊙O分别与AB、AC相切于E、F两点,BG是⊙O的切线,切点为G,则BG的长为$\frac{11}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
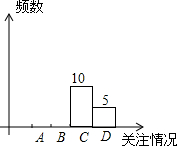 2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.
2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.| 关注情况 | 频数 | 频率 |
| A.高度关注 | k | 0.2 |
| B.一般关注 | m | 0.5 |
| C.极少关注 | 10 | n |
| D.不关注 | 5 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com