
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
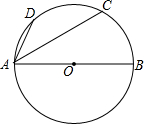 如图,AB为⊙O的直径,C、D为⊙O上的点,$\widehat{AD}$=$\widehat{CD}$.若∠CAB=40°,则∠CAD=25°.
如图,AB为⊙O的直径,C、D为⊙O上的点,$\widehat{AD}$=$\widehat{CD}$.若∠CAB=40°,则∠CAD=25°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
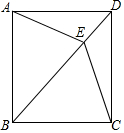 已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定?ABCD是菱形的只有( )
如图,在?ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定?ABCD是菱形的只有( )| A. | AC⊥BD | B. | AB=BC | C. | AC=BD | D. | ∠1=∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
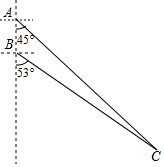 如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,$\sqrt{2}$≈1.41)
如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10%x=330 | B. | (1-10%)x=330 | C. | (1-10%)2x=330 | D. | (1+10%)x=330 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
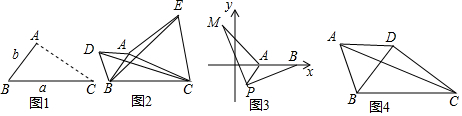
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com