
如图①, 已知抛物线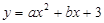 (a≠0)与
(a≠0)与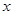 轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
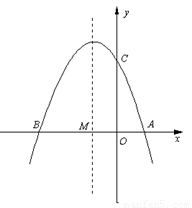
(1) 求抛物线的解析式;
(2) 点D的坐标为(-2,0).问:直线AC上是否存在点F,使得△ODF是等腰三角形?若存在,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
(3) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求△BCE面积的最大值,并求此时E点的坐标.
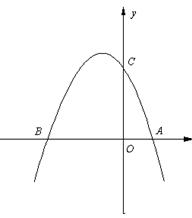
(1) 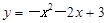 (2)
存在符合条件的点P, 其坐标为P (-1, 2 )或P(-
(2)
存在符合条件的点P, 其坐标为P (-1, 2 )或P(-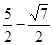 ,
,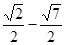 )或P(-
)或P(-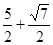 ,
,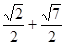 )(3)
最大值为
)(3)
最大值为 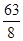 ,点E 坐标为 (-
,点E 坐标为 (-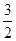 ,
,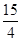 )
)
【解析】解: (1)由题知: 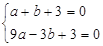 解得:
解得: 
∴ 所求抛物线解析式为: 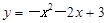 ……3分
……3分
(2) 存在符合条件的点P, 其坐标为P
(-1, 2 )或P(-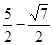 ,
,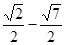 )
)
或P(-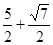 ,
,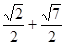 )……3分
)……3分
(3)过点E 作EF⊥x 轴于点F , 设E ( a
,-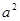 -2a+3 )( -3< a < 0 )
-2a+3 )( -3< a < 0 )
∴EF=-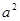 -2a+3,BF=a+3,OF=-a
-2a+3,BF=a+3,OF=-a
∴S四边形BOCE = 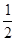 BF·EF +
BF·EF + 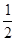 (OC
+EF)·OF
(OC
+EF)·OF
=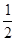 (
a+3 )·(-
(
a+3 )·(-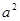 -2a+3) +
-2a+3) + 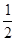 (-
(-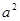 -2a+6)·(-a)
-2a+6)·(-a)
= =-
=-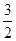
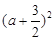 +
+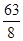
∴ 当a =-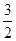 时,S四边形BOCE 最大, 且最大值为
时,S四边形BOCE 最大, 且最大值为 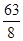 .……3分
.……3分
∴S四边形BOCE-S△ABC =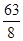 -6=
-6=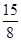
∴点E 坐标为 (-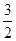 ,
,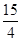 )……1分
)……1分
(1)由抛物线y=ax2+bx-3(a≠0)点A(1,0)和点B (-3,0),由待定系数法就可以直接求出a、b的值而求出抛物线的解析式.
(2)由(1)的解析式就可以求出C点的坐标,求出OC的值,在Rt△CON中由勾股定理就可以求出CN的值,CP1=NP1时,
作P1H⊥CN于H,由三角形相似就可以求出P1N的值,从而求出P1的坐标;
(3)设出点E的坐标,连接BE、CE,作EG⊥OB于点G,就可以表示EG、BG、OG的值就可以表示出四边形BOCE的面积,然后化为顶点式就可以求出其面积的最大值.


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com