
如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处测得塔顶仰角∠ACB=30°
(1)若河宽BC是60米,求塔AB的高(精确到0.1米;参考数据)
(2)若河宽BC无法度量.则应如何测量塔AB的高度呢?小明想出了另外一种方法:从点C出发,沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走a米到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高。

科目:初中数学 来源: 题型:
杭州湾跨海大桥两主塔与它们之间的斜拉索构成美轮美奂的对称造型,现测得跨海大桥主塔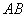 、
、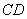 之间的距离
之间的距离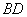 为
为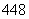 米,主塔
米,主塔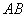 的一根斜拉索
的一根斜拉索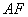 的仰角为
的仰角为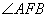
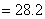 °,且
°,且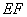 的长度为
的长度为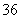 米,求该桥的主塔
米,求该桥的主塔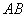 高为多少米?(精确到米,sin28.2°≈0.473,cos28.2°≈0.881,tan28.2°≈0.536)
高为多少米?(精确到米,sin28.2°≈0.473,cos28.2°≈0.881,tan28.2°≈0.536)


查看答案和解析>>
科目:初中数学 来源: 题型:
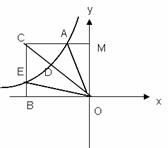
已知反比例函数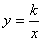 在第二象限内的图象如图所示,经过图象上两点A、E分别引
在第二象限内的图象如图所示,经过图象上两点A、E分别引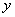 轴与
轴与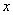 轴的垂线,交于点C,且与
轴的垂线,交于点C,且与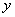 轴与
轴与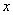 轴分别交于点M、B.连接OC交反比例函数图象于点D,且
轴分别交于点M、B.连接OC交反比例函数图象于点D,且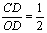 ,连接OA,OE,如果△AOC的面积是15,则△ADC与△BOE的面积和为
,连接OA,OE,如果△AOC的面积是15,则△ADC与△BOE的面积和为
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
|
| A.2a+b | <0 | B. | 3a+c<0 | C. | a+b+c>0 | D. | 4ac﹣b2<0 |
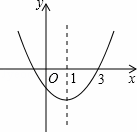
查看答案和解析>>
科目:初中数学 来源: 题型:
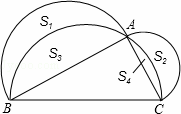
在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作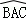 ,如图所示.若AB=4,AC=2,S1﹣S2=
,如图所示.若AB=4,AC=2,S1﹣S2=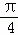 ,则S3﹣S4的值是 (改编)
,则S3﹣S4的值是 (改编)
查看答案和解析>>
科目:初中数学 来源: 题型:
根据国际货币基金组织IMF的预测数据,2013年世界各国GDP排名最高的仍为头号经济强国美国,其经济总量将达16万1979亿美元;中国位居第二,GDP总量为9万零386亿美元, 则中国的GDP总量用科学记数法可表示为( )亿美元
A.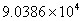 B.
B.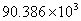 C.
C.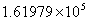 D.
D.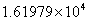
查看答案和解析>>
科目:初中数学 来源: 题型:
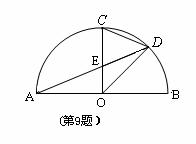
如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论:①∠DOB=∠ADC;②CE=OE;③△ODE∽△ADO;④2CD2=CE·AB.其中正确结论的序号是( )
A.①③ B.②④ C.①④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
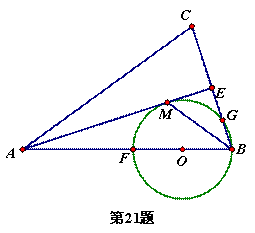
已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=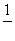 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com