
科目: 来源: 题型:
【题目】抛物线y=﹣x2+4ax+b(a>0)与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.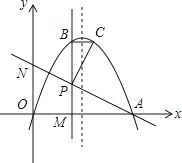
(1)a= ![]() 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;
(2)如图a>1时,若AP⊥PC,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.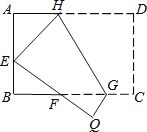
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,C,E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A,B两点,又分别以A,B为圆心,大于 ![]() AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是( )
AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是( ) 
A.CD⊥l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
查看答案和解析>>
科目: 来源: 题型:
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( ) 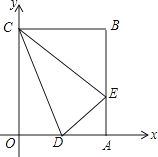
A.(3,1)
B.(3, ![]() )
)
C.(3, ![]() )
)
D.(3,2)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,DC=3,动点P从点A出发,沿A→D→C→B方向移动,动点Q从点A出发,在AB边上移动.设点P移动的路程为x,点Q移动的路程为y,线段PQ平分梯形ABCD的周长.
(1)求y与x的函数关系式,并求出x,y的取值范围;
(2)当PQ∥AC时,求x,y的值;
(3)当P不在BC边上时,线段PQ能否平分梯形ABCD的面积?若能,求出此时x的值;若不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车为1440辆;当每辆次小车的停车费超过5元时,每增加1元,到此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费一每天的固定支出)
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F. 
(1)求证:BP=DP;
(2)如图2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明;
(3)试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连接,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com