【题目】解方程组和分式方程：
（1）
（2） ．

【题目】在平面直角坐标系xOy中，已知第一象限内的点A在反比例函数 的图象上，第二象限内的点B在反比例函数 的图象上，连接OA、OB，若OA⊥OB，OB= OA，则k= ．

【题目】如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则DC= ．

给出了结论：
1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；
2）当 时，y＜0；
3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是（ ）
A.3
B.2
C.1
D.0

【题目】如图，在△ABC中，∠C=90°，BC=3，AB=5．点P从点B出发，以每秒1个单位长度沿B→C→A→B的方向运动；点Q从点C出发，以每秒2个单位沿C→A→B方向的运动，到达点B后立即原速返回，若P、Q两点同时运动，相遇后同时停止，设运动时间为t秒．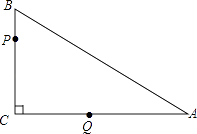

（1）当t=时，点P与点Q相遇；
（2）在点P从点B到点C的运动过程中，当t为何值时，△PCQ为等腰三角形？
（3）在点Q从点B返回点A的运动过程中，设△PCQ的面积为S平方单位．
①求S与t之间的函数关系式；
②当S最大时，过点P作直线交AB于点D，将△ABC中沿直线PD折叠，使点A落在直线PC上，求折叠后的△APD与△PCQ重叠部分的面积．

【题目】甲、乙两地之间有一条笔直的公路L，小明从甲地出发沿公路L步行前往乙地，同时小亮从乙地出发沿公路L骑自行车前往甲地，小亮到达甲地停留一段时间，原路原速返回，追上小明后两人一起步行到乙地．设小明与甲地的距离为y1米，小亮与甲地的距离为y2米，小明与小亮之间的距离为s米，小明行走的时间为x分钟．y1、y2与x之间的函数图象如图1，s与x之间的函数图象（部分）如图2．
（1）求小亮从乙地到甲地过程中y2（米）与x（分钟）之间的函数关系式；
（2）求小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式；
（3）在图2中，补全整个过程中s（米）与x（分钟）之间的函数图象，并确定a的值．

【题目】如图，AB是⊙O的直径，C是⊙O上的一点，直线MN经过点C，过点A作直线MN的垂线，垂足为点D，且∠BAC=∠DAC．
（1）猜想直线MN与⊙O的位置关系，并说明理由；
（2）若CD=6，cos∠ACD= ，求⊙O的半径．

【题目】一个不透明的袋子中装有大小、质地完全相同的3只球，球上分别标有2，3，5三个数字．
（1）从这个袋子中任意摸一只球，所标数字是奇数的概率是；
（2）从这个袋子中任意摸一只球，记下所标数字，不放回，再从从这个袋子中任意摸一只球，记下所标数字．将第一次记下的数字作为十位数字，第二次记下的数字作为个位数字，组成一个两位数．求所组成的两位数是5的倍数的概率．（请用“画树状图”或“列表”的方法写出过程）

解答下列问题：
（1）本次调查中的样本容量是；
（2）a= ， b=；
（3）试估计上述1000名学生中最喜欢羽毛球运动的人数．