
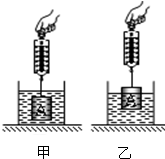
 底面积为100cm2的柱形容器中装有适量的水.当物体A如图甲所示,浸没在水中静止时,弹簧测力计的示数为F1=0.8N,水对杯底的压强为p1;向上提物体A,当A如图乙所示,总体积的
底面积为100cm2的柱形容器中装有适量的水.当物体A如图甲所示,浸没在水中静止时,弹簧测力计的示数为F1=0.8N,水对杯底的压强为p1;向上提物体A,当A如图乙所示,总体积的 露出水面静止时,容器中的水面降低了8mm,弹簧测力计的示数为F2,水对杯底的压强为p2.下列计算结果正确的是
露出水面静止时,容器中的水面降低了8mm,弹簧测力计的示数为F2,水对杯底的压强为p2.下列计算结果正确的是 排开水的体积,进一步求出金属块的体积;
排开水的体积,进一步求出金属块的体积; =
=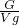 求出金属块的密度.
求出金属块的密度. 体积排开水的体积:
体积排开水的体积: V金,
V金,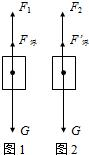
 F浮=
F浮= ×3.2N=2.4N,
×3.2N=2.4N, =
=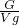 =
=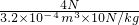 =1.25×103kg/m3,故B正确.
=1.25×103kg/m3,故B正确.

科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
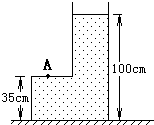 如图所示,在质量为1kg的容器内装有5kg的水,容器底面积为100cm2,容器放在水平桌面上,桌面面积为0.9m2(g取10N/kg),求:
如图所示,在质量为1kg的容器内装有5kg的水,容器底面积为100cm2,容器放在水平桌面上,桌面面积为0.9m2(g取10N/kg),求:查看答案和解析>>
科目:初中物理 来源: 题型:
 一边长为2cm的正方体实心铝块,密度为2.7×103kg/m3,先按图甲所示把铝块挂在弹簧测力计下静止,然后按图乙所示用弹簧秤吊着慢慢浸没在盛水的容器中,容器的底面积为100cm2,铝块浸没后水末溢出,g取10N/kg.根据以上提供的数据和物理情景,可以求出哪些物理量?(求出五个物理量即可,要求写出详细求解过程)
一边长为2cm的正方体实心铝块,密度为2.7×103kg/m3,先按图甲所示把铝块挂在弹簧测力计下静止,然后按图乙所示用弹簧秤吊着慢慢浸没在盛水的容器中,容器的底面积为100cm2,铝块浸没后水末溢出,g取10N/kg.根据以上提供的数据和物理情景,可以求出哪些物理量?(求出五个物理量即可,要求写出详细求解过程)查看答案和解析>>
科目:初中物理 来源: 题型:
 底面积为100cm2的柱形容器中装有适量的水.当金属块A如图甲所示,浸没在水中静止时,弹簧测力计的示数为F1=0.8N,水对杯底的压强为p1;向上提金属块A,当金属块A如图乙所示,总体积的
底面积为100cm2的柱形容器中装有适量的水.当金属块A如图甲所示,浸没在水中静止时,弹簧测力计的示数为F1=0.8N,水对杯底的压强为p1;向上提金属块A,当金属块A如图乙所示,总体积的| 1 |
| 4 |
查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,容器的底面积为100cm2,放在水平桌面上,容器内装有重45N、深40cm的水(水的密度ρ水=103kg/m3,g取10N/kg)
如图所示,容器的底面积为100cm2,放在水平桌面上,容器内装有重45N、深40cm的水(水的密度ρ水=103kg/m3,g取10N/kg)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com