
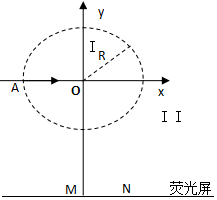
 如图所示,圆心为原点、半径为R的圆将xOy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ.区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1.平行于x轴的荧光屏垂直于xOy平面,放置在坐标y=-2.2R的位置.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(-R,0)的A点沿x正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变.若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的 N点.不计重力和粒子间的相互作用,求:
如图所示,圆心为原点、半径为R的圆将xOy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ.区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1.平行于x轴的荧光屏垂直于xOy平面,放置在坐标y=-2.2R的位置.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(-R,0)的A点沿x正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变.若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的 N点.不计重力和粒子间的相互作用,求:分析 (1)粒子在磁场中洛伦兹力不做功,粒子的动能不变,根据动能的大小求出粒子的速度大小.
(2)抓住粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,根据荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变,得出粒子在磁场区域Ⅰ中的轨迹,结合半径公式求出磁场的磁感应强度大小,根据偏转方向确定磁场的方向;根据粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的 N点,作出轨迹,根据几何关系求出半径,从而得出磁感应强度的大小和方向.
(3)作出粒子的运动的轨迹,抓住粒子须由II区再到A点才完成一个周期,通过几何关系,结合粒子在磁场中的运动时间求出粒子从A点沿x轴正方向射入区域Ⅰ后的运动周期.
解答 解:(1)粒子在磁场中运动时洛伦兹力不做功,打在M点和N点的粒子动能均为E0,速度v1、v2大小相等,设为v,由E0=$\frac{1}{2}$mv2
得:v=$\sqrt{\frac{2{E}_{0}}{m}}$.
(2)如图所示,区域Ⅱ中无磁场时,粒子在区域Ⅰ中运动四分之一圆周后,从C点沿y轴负方向打在M点,轨迹圆心是O1点,半径为:r1=R,区域Ⅱ有磁场时,粒子轨迹圆心是O2点,半径为r2,由几何关系得:r=(1.2R)2+(r2-0.4R)2,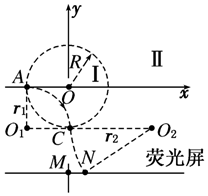 ;
;
解得:r2=2R
由qvB=m$\frac{{v}^{2}}{r}$得:B=$\frac{mv}{qr}$;故有:B1=$\frac{\sqrt{2{mE}_{0}}}{qR}$,方向垂直xOy平面向外.
B2=$\frac{\sqrt{2m{E}_{0}}}{2qR}$,方向垂直xOy平面向里.
(3)如图,由qvB=m$\frac{{v}^{2}}{r}$得得在II区的半径为:r3=$\frac{{r}_{1}}{\sqrt{3}}$=$\frac{\sqrt{3}R}{3}$,得:θ=60°;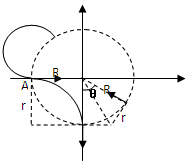 ;
;
粒子须由II区再到A点才完成一个周期,故有:360n=(90+60)n',
$\frac{n}{n'}$=$\frac{5}{12}$,T=($\frac{1}{4}$×$\frac{2π{r}_{1}}{v}$+$\frac{2}{3}$×$\frac{2π{r}_{3}}{v}$)×12,
代入数据得:T=$\frac{(18+16\sqrt{3})πR}{3}\sqrt{\frac{m}{2{E}_{0}}}$.
答:(1)打在M点和N点的粒子运动速度v1、v2的大小均为$\sqrt{\frac{2{E}_{0}}{m}}$;(2)B1=$\frac{\sqrt{2{mE}_{0}}}{qR}$,方向垂直xOy平面向外;B2=$\frac{\sqrt{2m{E}_{0}}}{2qR}$,方向垂直xOy平面向里;(3)粒子从A点沿x轴正方向射入区域Ⅰ后的运动周期为T=$\frac{(18+16\sqrt{3})πR}{3}\sqrt{\frac{m}{2{E}_{0}}}$.
点评 处理带电粒子在磁场中的运动问题,关键作出粒子的运动轨迹,确定圆心、半径和圆心角是基础,通过半径公式和周期公式,结合几何关系进行求解.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:选择题
 如图所示,位于一水平面内的、两根平行的光滑金属导轨,处在匀强磁场中,磁场方向垂直于导轨所在的平面,导轨的一端与一电阻相连;具有一定质量的金属杆ab放在导轨上并与导轨垂直.现用一平行于导轨的恒力F拉杆ab,使它由静止开始向右运动.杆和导轨的电阻、感应电流产生的磁场均可不计.用E表示回路中的感应电动势,I表示回路中的感应电流,在I随时间增大的过程中,电阻消耗的功率等于( )
如图所示,位于一水平面内的、两根平行的光滑金属导轨,处在匀强磁场中,磁场方向垂直于导轨所在的平面,导轨的一端与一电阻相连;具有一定质量的金属杆ab放在导轨上并与导轨垂直.现用一平行于导轨的恒力F拉杆ab,使它由静止开始向右运动.杆和导轨的电阻、感应电流产生的磁场均可不计.用E表示回路中的感应电动势,I表示回路中的感应电流,在I随时间增大的过程中,电阻消耗的功率等于( )| A. | F的功率 | B. | 安培力的功率的绝对值 | ||
| C. | F与安培力的合力的功率 |
查看答案和解析>>
科目:初中物理 来源: 题型:实验探究题
| 位置 | A | B | C |
| 电流I/A | 0.30 | 0.24 | 0.54 |
查看答案和解析>>
科目:初中物理 来源: 题型:作图题
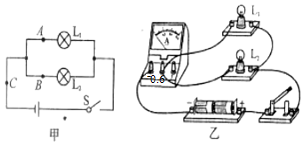
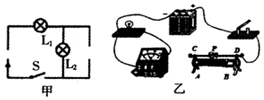 (1)在图甲所示的电路中,根据标出的电流方向,从电源、电流表、电压表三个元件符号中选出两个,并分别填进电路的空缺处.要求:灯泡L1和L2串联.
(1)在图甲所示的电路中,根据标出的电流方向,从电源、电流表、电压表三个元件符号中选出两个,并分别填进电路的空缺处.要求:灯泡L1和L2串联.查看答案和解析>>
科目:初中物理 来源: 题型:选择题
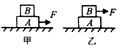 如图所示,叠放在一起的物体A和B,在大小为F=10N的恒力作用下,10s内沿水平方向匀速直线运动1m,下列结论中正确的是( )
如图所示,叠放在一起的物体A和B,在大小为F=10N的恒力作用下,10s内沿水平方向匀速直线运动1m,下列结论中正确的是( )| A. | 甲、乙两图中物体B所受摩擦力大小均为10N | |
| B. | 甲、乙两图中物体A受到地面对它的摩擦力大小均为10N | |
| C. | 甲图中,力F做功1J | |
| D. | 乙图中,力F做功的功率为10W |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com