
 如图:AB为一根均匀轻质杆,杆的中点O点悬挂在天花板上,在杆的A端悬挂有一端开口、粗细均匀、重2N的薄壁玻璃管,管长L=40cm,管底面积S=20cm2,管中装满水后倒扣在装有水深h=10cm的水槽中,玻璃管管口刚好被水面淹没,在杠杆的B端通过滑轮组用轻质细绳相连,动滑轮下端挂有一个钩码,在滑动组的另一端细绳上挂有一体积为103cm3的实心均匀圆球,当圆球体积的一半浸没在水中时,杠杆恰好在水平位置平衡.已知大气压强P0=105Pa,动滑轮重1N,细绳的重量和细绳与滑轮间的摩擦忽略不计,g=10N/kg. 求:
如图:AB为一根均匀轻质杆,杆的中点O点悬挂在天花板上,在杆的A端悬挂有一端开口、粗细均匀、重2N的薄壁玻璃管,管长L=40cm,管底面积S=20cm2,管中装满水后倒扣在装有水深h=10cm的水槽中,玻璃管管口刚好被水面淹没,在杠杆的B端通过滑轮组用轻质细绳相连,动滑轮下端挂有一个钩码,在滑动组的另一端细绳上挂有一体积为103cm3的实心均匀圆球,当圆球体积的一半浸没在水中时,杠杆恰好在水平位置平衡.已知大气压强P0=105Pa,动滑轮重1N,细绳的重量和细绳与滑轮间的摩擦忽略不计,g=10N/kg. 求: (G动+G钩)
(G动+G钩)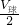 +FB;
+FB; (G动+G钩)来求得.而作用在B端的拉力可以利用杠杆的平衡条件去求得.
(G动+G钩)来求得.而作用在B端的拉力可以利用杠杆的平衡条件去求得.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中物理 来源: 题型:
 如图:AB为一根均匀轻质杆,杆的中点O点悬挂在天花板上,在杆的A端悬挂有一端开口、粗细均匀、重2N的薄壁玻璃管,管长L=40cm,管底面积S=20cm2,管中装满水后倒扣在装有水深h=10cm的水槽中,玻璃管管口刚好被水面淹没,在杠杆的B端通过滑轮组用轻质细绳相连,动滑轮下端挂有一个钩码,在滑动组的另一端细绳上挂有一体积为103cm3的实心均匀圆球,当圆球体积的一半浸没在水中时,杠杆恰好在水平位置平衡.已知大气压强P0=105Pa,动滑轮重1N,细绳的重量和细绳与滑轮间的摩擦忽略不计,g=10N/kg. 求:
如图:AB为一根均匀轻质杆,杆的中点O点悬挂在天花板上,在杆的A端悬挂有一端开口、粗细均匀、重2N的薄壁玻璃管,管长L=40cm,管底面积S=20cm2,管中装满水后倒扣在装有水深h=10cm的水槽中,玻璃管管口刚好被水面淹没,在杠杆的B端通过滑轮组用轻质细绳相连,动滑轮下端挂有一个钩码,在滑动组的另一端细绳上挂有一体积为103cm3的实心均匀圆球,当圆球体积的一半浸没在水中时,杠杆恰好在水平位置平衡.已知大气压强P0=105Pa,动滑轮重1N,细绳的重量和细绳与滑轮间的摩擦忽略不计,g=10N/kg. 求:查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,一根均匀的木条AB长为L.将其放在水平桌面上,使B端伸出桌面
如图所示,一根均匀的木条AB长为L.将其放在水平桌面上,使B端伸出桌面| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中物理 来源:2013届湖北省鄂州市第三中学九年级上学期期中考试物理试卷(带解析) 题型:填空题
如图所示,一根均匀的木条AB长为L。将其放在水平桌面上,使B端伸出桌面 L,在伸出桌面部分的上方放一个长
L,在伸出桌面部分的上方放一个长 L,重3N的均匀木块恰能使A端离开桌面,则木条重 N。
L,重3N的均匀木块恰能使A端离开桌面,则木条重 N。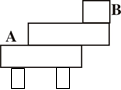
查看答案和解析>>
科目:初中物理 来源:2012-2013学年湖北省鄂州市九年级上学期期中考试物理试卷(解析版) 题型:填空题
如图所示,一根均匀的木条AB长为L。将其放在水平桌面上,使B端伸出桌面 L,在伸出桌面部分的上方放一个长
L,在伸出桌面部分的上方放一个长 L,重3N的均匀木块恰能使A端离开桌面,则木条重 N。
L,重3N的均匀木块恰能使A端离开桌面,则木条重 N。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com