
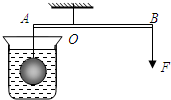
 如图所示,杠杆AOB处在水平位置平衡,OA:OB=1:2,浸入水中的铁球质量m=7.9千克,加在B端的力F=24.5牛,ρ铁=7.9×103千克/米3,g=10N/Kg.则空心体积为________m3.
如图所示,杠杆AOB处在水平位置平衡,OA:OB=1:2,浸入水中的铁球质量m=7.9千克,加在B端的力F=24.5牛,ρ铁=7.9×103千克/米3,g=10N/Kg.则空心体积为________m3. =
=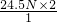 =49N,
=49N,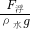 =
= =3×10-3m3,
=3×10-3m3, ,∴7.9kg铁的体积:
,∴7.9kg铁的体积: =
=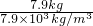 =1×10-3m3,
=1×10-3m3,

科目:初中物理 来源: 题型:
 6、如图所示,杠杆AOB用细线悬挂起来,当A端挂重GA的物体,B端挂重GB的物体时,杠杆处于平衡状态,此时OA恰好处于水平位置,AO=BO,杠杆重不计,则( )
6、如图所示,杠杆AOB用细线悬挂起来,当A端挂重GA的物体,B端挂重GB的物体时,杠杆处于平衡状态,此时OA恰好处于水平位置,AO=BO,杠杆重不计,则( )查看答案和解析>>
科目:初中物理 来源: 题型:

查看答案和解析>>
科目:初中物理 来源: 题型:
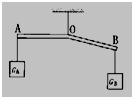 如图所示,杠杆AOB的A端挂重为G.的物体,B端挂重为G的物体,杠杆平衡时AO处于水平位置,若AO=BO,杠杆自重不计,则GA和GB的大小关系是、GA
如图所示,杠杆AOB的A端挂重为G.的物体,B端挂重为G的物体,杠杆平衡时AO处于水平位置,若AO=BO,杠杆自重不计,则GA和GB的大小关系是、GA查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com