Question

请按要求作出各图（作图时请用铅笔、直尺并保留作图痕迹）
（1）在图1中画出人看到球的光路图

（2）如图2所示，MN为平面镜，O为人眼在平面镜前的位置，A、B、C、D四个物点中，人眼看不到哪个物点所成的像？
（3）画出图3中的平面镜，标出入射角α和反射角β；

（4）如图4所示，B为隧道中的一堵墙，墙的左侧有一激光器S，发出一束激光经平面镜MN反射后恰好经过A点，请根据平面镜成像特点画出符合要求的入射光线和反射光线．

（5）如图5所示a、b是经平面镜反射后的反射光线，画出对应的入射光线．
（6）如图6所示，水平地面上有一障碍物ABCD，较大的平面镜MN在某一高度上水平放置，
①试用作图法求出眼睛位于O点从平面镜中所能看到的障碍物后方地面的范围；
②如果想在原处看到更大范围的地面，水平放置的镜子该怎样改变？

Answer 1

解：（1）作出球关于镜面的对称图，即为它的像，连接像与人眼，交镜面于一点O，即为入射点．再完成光路，如图所示．

（2）作O点关于平面镜成像的像点O′，分别连接OA′、OB′、OC′、OD′各点，如图所示：

发现只有连线O′D与平面镜无交点，所以其中不能看到的是放置在D点上的物体．
（3）由光反射定律知，反射角等于入射角，所以先做出反射光线与入射光线的夹角的平分线，然后再过入射点作这个角平分线的垂线即可．如图所示：

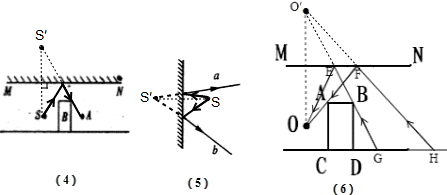
（4）根据平面镜成像时像与物关于平面镜对称，作出S点的像点S′，连接S′A交平面镜于点O，连接SO为入射光线，OA为反射光线；如图所示：
（5）先将两条反射光线反向延长交于一点S′，再作出S′关于平面镜的对称点S，即为发光点的位置，从反光点S到反射点画出两条入射光线，如图所示：
（6）①将O点看成是一个发光点．作O点在平面镜中的像O′，连接OA交MN于F，连接O′F交地面于H；连接O′B交MN于E，交地面于G，连接OE，标上箭头，光线传播方向如图所示．入射光线为HF、GE；反射光线为FO、EO．图中GH所围区域就是眼睛位于O点从平面镜MN中所能看到障碍物后方地面的范围．
②假定水平放置的镜子的高度降低至与障碍AB面接触，眼睛就看不到障碍物后面的地面，因此，如果想在原处看到更大范围的地面，水平放置的镜子在高度该增高（即向上移动）．

分析：（1）由平面镜的成像特点知，像与物关于镜面对称，且像是由光的反射光线的延长线形成的，故作出物关于镜面的对称图，即为它的像，连接像与人眼，交镜面于一点，即为入射点．再完成光路．
（2）作O点关于平面镜成像的像点O′，分别连接像点O′与A、B、C、D各点，如果连线与平面镜有交点，则能看到，否则不能．
（3）根据光的反射定律知，反射角等于入射角，故反射光线与入射光线的夹角的平分线是法线的位置，再过入射点作出法线的垂线，就是平面镜所在的位置．
（4）根据平面镜成像的特点知，反射光线好像是由像点发出的，由物与像关于镜面对称，作出像点后，作反射光线S′A与镜面的交点为入射点，再完成光路．
（5）根据反射光线反向延长通过像点，像与物关于平面镜对称，作出发光点S的位置，从发光点到反射点画出两条入射光线．
（6）①通过平面镜看到某部分地面，表明这部分地面上每一点发出的光线中有一些经平面镜反射后到达眼睛即O点．则由光路可逆性原理可知，若在O点放置点光源，它发出的光线经平面镜反射后将到达地面上这部分范围．
②如果平面镜MN的高度降低至与障碍AB面接触，则眼睛就看不到障碍物后面的地面，然后可知水平放置的镜子的高度该怎样调节．
点评：（1）平面镜成像的特点：像与物大小相等，连线与镜面垂直，到平面镜的距离相等，左右相反，即像与物关于平面镜对称；会利用平面镜成像的特点作图．
（2）根据光的反射定律作图，关键是对光的反射定律的理解，知道入射角和反射角是入射光线和反射光线与法线的夹角．
（3）光路可逆原理是光学知识中的基本原理，用“光路可逆原理“解答一些复杂的光学问题，显得相当简捷明快．