
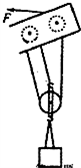
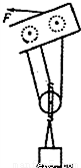
 如图所示的是建筑工地上正在运行的一台起重机吊臂上的滑轮组,由电动机向滑轮组提供动力,不计一切摩擦和绳重,已知动滑轮和吊钩共重200N,在拉力F的作用下,把重2.98×104N的重物匀速提高20m,拉力做功的功率为1.5×104W,求:
如图所示的是建筑工地上正在运行的一台起重机吊臂上的滑轮组,由电动机向滑轮组提供动力,不计一切摩擦和绳重,已知动滑轮和吊钩共重200N,在拉力F的作用下,把重2.98×104N的重物匀速提高20m,拉力做功的功率为1.5×104W,求: =
= ≈99.3%.
≈99.3%.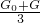 =
=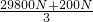 =10000N,
=10000N,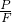 =
=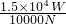 =1.5m/s.
=1.5m/s.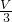 =
= =0.5m/s.
=0.5m/s. 求出效率.
求出效率.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中物理 来源: 题型:
 如图所示,是建筑工地常用来搬运砖块的两种机械(滑轮组和起重机).观察丙图和
如图所示,是建筑工地常用来搬运砖块的两种机械(滑轮组和起重机).观察丙图和查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示的是建筑工地上正在运行的一台起重机吊臂上的滑轮组,由电动机向滑轮组提供动力,不计一切摩擦和绳重,已知动滑轮和吊钩共重200N,在拉力F的作用下,把重2.98×104N的重物匀速提高20m,拉力做功的功率为1.5×104W,求:
如图所示的是建筑工地上正在运行的一台起重机吊臂上的滑轮组,由电动机向滑轮组提供动力,不计一切摩擦和绳重,已知动滑轮和吊钩共重200N,在拉力F的作用下,把重2.98×104N的重物匀速提高20m,拉力做功的功率为1.5×104W,求:查看答案和解析>>
科目:初中物理 来源:2008年江苏省苏州市吴江市桃源中学中考物理二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com