
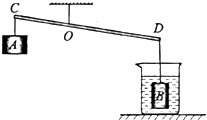
 如图是小红利用杠杆提升浸没在水中的物体B的示意图,杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,烧杯的底面积为80cm2,物体B的质量是320克,体积是60cm2.当物体B浸没在水中时,水对烧杯底的压强为p1.当用力拉A,将物体B从烧杯底提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉A的力为3N,烧杯中的水对杯底的压强为p2.若P1与p2之差为50Pa.则物体A的质量是________g.(g取10N/kg,杠杆的质量、悬挂物体A和物体B的细绳的质量均忽略不计)
如图是小红利用杠杆提升浸没在水中的物体B的示意图,杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,烧杯的底面积为80cm2,物体B的质量是320克,体积是60cm2.当物体B浸没在水中时,水对烧杯底的压强为p1.当用力拉A,将物体B从烧杯底提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉A的力为3N,烧杯中的水对杯底的压强为p2.若P1与p2之差为50Pa.则物体A的质量是________g.(g取10N/kg,杠杆的质量、悬挂物体A和物体B的细绳的质量均忽略不计)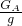 =
=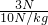 =0.3kg=300g;
=0.3kg=300g;

科目:初中物理 来源: 题型:
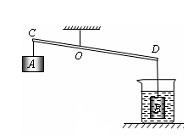 如图是小华利用杠杆提升浸没在水中的物体B的示意图.杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,其质量为200g.烧杯的底面积为75cm2,物体B的质量为320g,它的体积为40cm3.当物体B浸没在水中时,水对杯底的压强为P1.当用力拉物体A,将物体B提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉物体A的力为F,水对杯底的压强为P2.若p1与p2之差为40Pa,求拉力F的大小.(g取10N/kg,杠杆的质量、悬挂物体A和物体B的细绳的质量均忽略不计)
如图是小华利用杠杆提升浸没在水中的物体B的示意图.杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,其质量为200g.烧杯的底面积为75cm2,物体B的质量为320g,它的体积为40cm3.当物体B浸没在水中时,水对杯底的压强为P1.当用力拉物体A,将物体B提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉物体A的力为F,水对杯底的压强为P2.若p1与p2之差为40Pa,求拉力F的大小.(g取10N/kg,杠杆的质量、悬挂物体A和物体B的细绳的质量均忽略不计)查看答案和解析>>
科目:初中物理 来源: 题型:
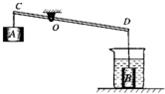 22、如图是小华利用杠杆提升浸没在水中的物体B的示意图.杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,其质量为200g.烧杯的底面积为75cm2,物体B的质量为320g,它的体积为40cm3.当物体B浸没在水中时,水对杯底的压强为p1.当用力拉物体A,将物体B提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉物体A的力为F,水对杯底的压强为p2.若p1与p2之差为40Pa,则拉力F的大小为
22、如图是小华利用杠杆提升浸没在水中的物体B的示意图.杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,其质量为200g.烧杯的底面积为75cm2,物体B的质量为320g,它的体积为40cm3.当物体B浸没在水中时,水对杯底的压强为p1.当用力拉物体A,将物体B提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉物体A的力为F,水对杯底的压强为p2.若p1与p2之差为40Pa,则拉力F的大小为查看答案和解析>>
科目:初中物理 来源: 题型:
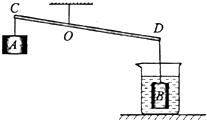 (2013?大兴区二模)如图是小红利用杠杆提升浸没在水中的物体B的示意图,杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,烧杯的底面积为80cm2,物体B的质量是320克,体积是60cm3.当物体B浸没在水中时,水对烧杯底的压强为p1.当用力拉A,将物体B从烧杯底提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉A的力为3N,烧杯中的水对杯底的压强为p2.若P1与p2之差为50Pa.则物体A的质量是
(2013?大兴区二模)如图是小红利用杠杆提升浸没在水中的物体B的示意图,杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,烧杯的底面积为80cm2,物体B的质量是320克,体积是60cm3.当物体B浸没在水中时,水对烧杯底的压强为p1.当用力拉A,将物体B从烧杯底提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉A的力为3N,烧杯中的水对杯底的压强为p2.若P1与p2之差为50Pa.则物体A的质量是查看答案和解析>>
科目:初中物理 来源:2013年北京市大兴区中考物理二模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com