;

;

;

分析:(1)质量分布均匀、形状规则的物体重心在其几何中心,据此确定砖的重心位置;
(2)砖块可以看做杠杆,由杠杆平衡条件知:只要上面的砖重心不超出支点之外,砖就可平衡.
(3)从上向下分析,求出各砖能伸出的最大长度.
解答:
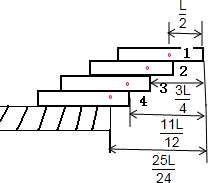
解:
没一块砖的长度为L,砖质量分布均匀,形状规则,其重心在其几何中心,;
(1)第1块砖的重心在距砖的右端

处,如图所示,第1块砖放在第2块砖上面,第2块砖的右端是第1块砖的支点,当第1块砖伸出的长度为

时,砖的重心恰好在支点上,第1块砖恰能平衡,如果砖伸出的长度大于

,砖将翻到,不会平衡,因此第1块砖伸出的最大长度是砖长的

.
(2)第1与第2块砖组成的整体重心在它们的几何中心,第3块砖的右端是它们的支点,它们重心距第1块砖最右端的距离是
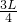
,如图所示,第1与第2块砖组成的整体重心距支点的距离为
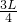
-

=

,则第2块砖伸出的最大长度是砖长的

.
(3)第1、2、3三块砖组成的整体重心位置距第1块砖的距离是
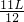
,如图所示,第4块砖的右端是上面3块砖的支点,
第1、2、3块砖的重心距它们支点的距离是
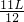
-
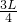
=
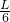
,所以第3块砖伸出的最大长度是砖长的

.
(4)4块砖组成的整体重心在它们的几何中心,它们的重心距第1块砖右端的距离是
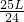
,如图所示,桌面是它们的支点,4块砖的重心距支点的距离是
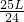
-
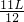
=
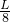
,第4块砖伸出的最大长度是砖长的

.
故答案为:

;

;

;

.
点评:本题考查了确定物体伸出的最大长度问题,难度较大,是一道难题;恰当地选择研究对象、确定研究对象的重心,是正确解题的关键.

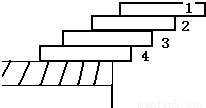
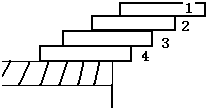 建筑工人用4块砖砌成屋顶的边缘,如图,使每一块砖压着下面的砖并伸出一部分,如果砖不用水泥粘紧而处于平衡,问各砖能伸出的最大长度分别是________.
建筑工人用4块砖砌成屋顶的边缘,如图,使每一块砖压着下面的砖并伸出一部分,如果砖不用水泥粘紧而处于平衡,问各砖能伸出的最大长度分别是________. ;
; ;
; ;
;
 解:
解: 处,如图所示,第1块砖放在第2块砖上面,第2块砖的右端是第1块砖的支点,当第1块砖伸出的长度为
处,如图所示,第1块砖放在第2块砖上面,第2块砖的右端是第1块砖的支点,当第1块砖伸出的长度为 时,砖的重心恰好在支点上,第1块砖恰能平衡,如果砖伸出的长度大于
时,砖的重心恰好在支点上,第1块砖恰能平衡,如果砖伸出的长度大于 ,砖将翻到,不会平衡,因此第1块砖伸出的最大长度是砖长的
,砖将翻到,不会平衡,因此第1块砖伸出的最大长度是砖长的 .
.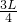 ,如图所示,第1与第2块砖组成的整体重心距支点的距离为
,如图所示,第1与第2块砖组成的整体重心距支点的距离为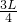 -
- =
= ,则第2块砖伸出的最大长度是砖长的
,则第2块砖伸出的最大长度是砖长的 .
.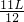 ,如图所示,第4块砖的右端是上面3块砖的支点,
,如图所示,第4块砖的右端是上面3块砖的支点,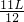 -
-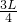 =
=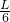 ,所以第3块砖伸出的最大长度是砖长的
,所以第3块砖伸出的最大长度是砖长的 .
.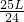 ,如图所示,桌面是它们的支点,4块砖的重心距支点的距离是
,如图所示,桌面是它们的支点,4块砖的重心距支点的距离是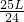 -
-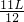 =
=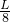 ,第4块砖伸出的最大长度是砖长的
,第4块砖伸出的最大长度是砖长的 .
. ;
; ;
; ;
; .
.

 全能练考卷系列答案
全能练考卷系列答案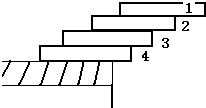 建筑工人用4块砖砌成屋顶的边缘,如图,使每一块砖压着下面的砖并伸出一部分,如果砖不用水泥粘紧而处于平衡,问各砖能伸出的最大长度分别是
建筑工人用4块砖砌成屋顶的边缘,如图,使每一块砖压着下面的砖并伸出一部分,如果砖不用水泥粘紧而处于平衡,问各砖能伸出的最大长度分别是