

 (G+G动-F浮)=
(G+G动-F浮)= (G+G动-F浮)-----------①
(G+G动-F浮)-----------① (G+G动)=
(G+G动)= (G+G动)-------------------②
(G+G动)-------------------②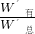 =
=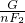 ,
,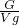 =
=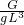 =
=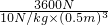 =2880kg/m3.
=2880kg/m3. =
=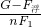 =
=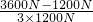 ≈66.7%.
≈66.7%. (G+G动-F浮)、F2=
(G+G动-F浮)、F2= (G+G动).然后代入数据即可求出浮力.
(G+G动).然后代入数据即可求出浮力. =
=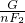 代入数据即可求出金属块重力,然后根据密度公式求金属块密度;
代入数据即可求出金属块重力,然后根据密度公式求金属块密度; =
=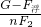 求机械效率.
求机械效率.

科目:初中物理 来源: 题型:

查看答案和解析>>
科目:初中物理 来源: 题型:
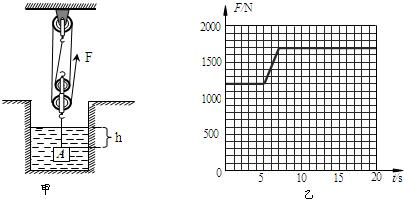
查看答案和解析>>
科目:初中物理 来源:2009年北京市房山区中考物理二模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中物理 来源:2011年北京市昌平区中考物理二模试卷(解析版) 题型:填空题
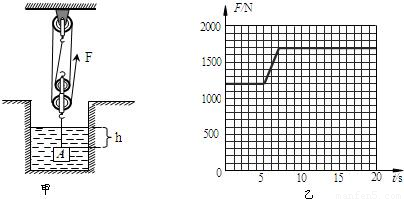
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com